Puzzles & Games with esProc: Eight Queens Puzzle
Eight queens puzzle is one of the chess puzzles that put eight queens on a 8×8 chessboard so that no queen attacks any others. Well, how many solutions are there?

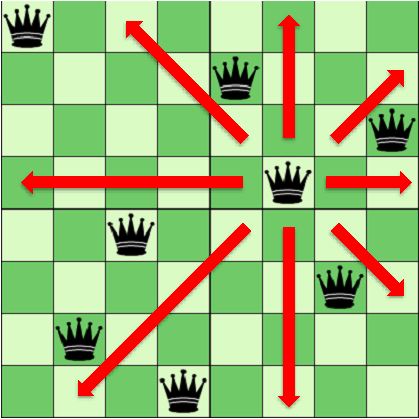
A queen attacks any other queen that sits on the same row, column or diagonal. A solution requires that no two queens share the same row, column or diagonal.
Since there is only one queen in each row, we can use a sequence of the length of 8 to set in turn the column number on which a queen on each row sits. For a row without a queen, that is, no column in this row has a queen - the column number is zero; every time when we put a queen on the board, if the column number is not one of the members of the sequence, then no other queen sits on the same column.
At the same time, we need to make sure there is no other queen on a diagonal when placing a new queen on it. If a queen sits on column k of row m, there are two squares at most on row m+n that share the same diagonal with it; the horizontal distance between either of the squares and the queen equals the vertical distance between them. This means there are two squares (m+n,k+n) and (m+n,k-n) at most share the same diagonal with it.
So, we will know the number of solutions by looking at all squares of a row on which a queen is placed. esProc handles this through a loop operation, as shown below:
A |
B |
C |
D |
|
1 |
=[0]*8 |
>i=1 |
||
2 |
for i>0 |
>A1(i)=A1(i)+1 |
||
3 |
if A1(i)==9 |
>A1(i)=0,i=i-1 |
next |
|
4 |
if i==1 |
>i=2 |
next |
|
5 |
=A1(i) |
=A1.to(i-1) |
||
6 |
if C5.pos(B5)>0 |
next |
||
7 |
else if C5.pselect(i-#==abs(B5-~))>0 |
next |
||
8 |
>i=i+1 |
|||
9 |
if i==9 |
>C1=C1|A1.conj@s() |
>A1(8)=0,i=7 |
|
10 |
=C1.len() |
Line 1: A1 is the sequence of column numbers recording the queens’ locations. B1 defines variable i to record the number of the current row where a queen is placed.
Line 2: Performs a traversal, moving a queen rightward through the squares of the current row.
Line 3: When a queen is moved to column 9, the traversal of all squares in the current row is completed. Now we reset the column number for the current row to zero and subtract 1 from i to begin a traversal on the next row. When traversal on all squares of the first row is finished, variable i’s value becomes zero and the loop exits.
Line 4: when moving the queen along the first row, there is no need to judge if a square is eligible for holding the queen; just place the second queen.
Line 6: Checks if there is any column shared by the settled queens.
Line 7: Finds if there is any diagonal shared by them. If results of both judgments are true, we can go on to place a queen on the next row.
When all the eight queens are settled, store their current places in line 9.
Here’s the result in A10:
![]()
We can see detailed result in C1:
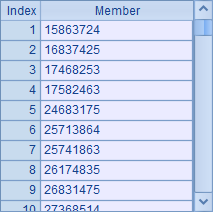
We can also solve the puzzle by recursively calling a subroutine:
A |
B |
C |
D |
E |
|
1 |
[] |
=func(A2,A1) |
=C1.len() |
||
2 |
func |
for 8 |
if func(A5,A2,B2) |
=A2|B2 |
|
3 |
if D2.len()==8 |
>C1=C1|D2.conj@s() |
|||
4 |
else |
>func(A2,D2) |
|||
5 |
func |
if A5.pos(B5)>0 |
return false |
||
6 |
for A5 |
if abs(B5-B6)==A5.len()+1-#B6 |
return false |
||
7 |
return true |
In A2’s subroutine, a queen is placed on a row and then B2 loops through every possible column.
The subroutine in A5 finds if a column in the current row is eligible for holding a queen. C5 checks if there is already a queen on this column. Line 6 checks if a queen already exists on the same diagonal, and if it does this column is ineligible. If the specified column is eligible, look at if the eight queens have all properly placed; if the return value is false, call A2’s subroutine recursively to move on to the next row to place a queen. Store places of the eight queens in C1 after they are all settled. This approach produces the same result but easier to understand code.
SPL Official Website 👉 https://www.scudata.com
SPL Feedback and Help 👉 https://www.reddit.com/r/esProcSPL
SPL Learning Material 👉 https://c.scudata.com
SPL Source Code and Package 👉 https://github.com/SPLWare/esProc
Discord 👉 https://discord.gg/2bkGwqTj
Youtube 👉 https://www.youtube.com/@esProc_SPL


