Puzzles & Games with esProc: The 24 Game
The 24 game is an arithmetical card game played with jokers removed. The rule is to draw four cards randomly and manipulate the four numbers to get the result 24 using four arithmetic operations, addition, subtraction, multiplication and division (parentheses are allowed). The face cards, Jack, Queen and King, correspond to numbers 11, 12 and 13 respectively.
With esProc, we can conveniently program the game (as the following SPL script 24points.dfx shows) and calculate the result with four random numbers.
A |
B |
C |
D |
|
1 |
=arg1 |
[+,-,*,/] |
[] |
[] |
2 |
=to(0,255).([~\64+1, ~%64\16+1,~%16\4+1,~%4+1]) |
=A2.select(~.id().count()==4) |
||
3 |
=to(0,63).([~\16+1, ~%16\4+1,~%4+1]) |
=A3.select(~.eq([1,2,3])) |
=A3.(~.(B1(~))) |
|
4 |
=B2.(~.(A1(~))) |
=A4.id() |
||
5 |
for B4 |
for B3 |
for C3 |
>func(A8,A5,B5,C5) |
6 |
=C1.id(~) |
for A6 |
if round(eval(B6),3) ==24 |
>D1=D1|B6 |
7 |
if D1.len()==0 |
>D1=”No answer.” |
||
8 |
func |
=A8.(~) |
||
9 |
=B8.(~) |
for B9 |
>B9.(~=~-if(#>#C9 && ~>C9,1,0)) |
|
10 |
for B9 |
=D8(B10)/C8(#B10)/ D8(B10+1) |
>D8.delete(B10) |
|
11 |
if #B10==3 |
>C1=C1&C10 |
||
12 |
else |
>D8(B10)=”(“/C10/”)” |
||
13 |
return D1 |
Parameter arg1 accepts the input of 4 numbers. Its value can be viewed in A1. 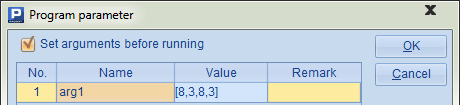
A1 defines four numbers to achieve 24, which are 8, 3, 8, and 3 in our case. First we try all possible permutations of the four cards. To do this, A2 lists the permutations, including those with repeated numbers, using a four-digit quaternary number. B2 selects those without repeated numbers:
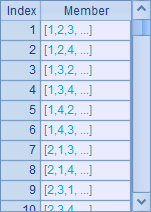
The calculation needs three arithmetic operators inserted between the four numbers. Each is a random one among addition, subtraction, multiplication and division. A3 gets three-digit quaternary numbers of all possible operator combinations iteratively:
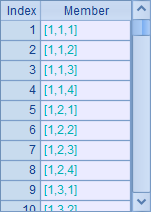
As different computational orders lead to different results, we can adjust the order by adding parentheses in different ways. Three operators mean the arithmetic is performed in three steps, and different ways of adding parentheses decide the order of the three steps. B3 selects from A3’s results the combinations containing all the three operators, 1, 2, 3. They are all possible execution orders, as shown below:
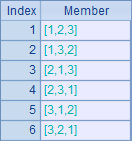
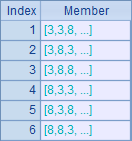
Since there could be repeated numbers among the four randomly selected cards, A4 lists all permutations of numbers and B4 removes the possible duplicate permutations to avoid redundant loops. Here’s B4’s result:
For each card permutation, the code in line 5 tries each combination of arithmetic operators in every computational order and calls A8’s subroutine to get all possible expressions whose result is 24.
At the call of A8’s subroutine, the sequence of numbers, the sequence of operators and the sequence of computational orders are assigned to A8, B8 and C8 respectively, and the expression for doing the arithmetic is stored in D8. After a card permutation tries all combinations of operators in a certain computational order, line 9 moves to another computational order. B10 performs a loop to do the arithmetic. For each step two card numbers or expressions are joined up with an operator, and at the same time a number or an expression in D8’s expression is eliminated. Line 11 makes a judgment. If it is the last step of the arithmetic, store the final expression to C1’s sequence; if it is an intermediate step, add parentheses to the newly-generated expression to change to another computational order and update it onto D8.
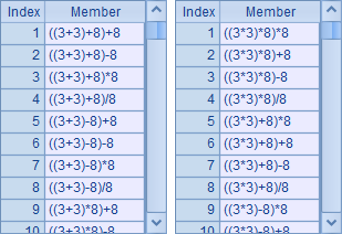
When line 5 finishes the subroutine call, C1 will have obtained the expressions of all possible calculations, including the duplicates, which will be removed by id() function in A6. Here’re the sequences of expressions in C1 and A6 respectively:
B6 loops through each expression in A6 to find with eval() function if their result is 24. Considering the computational error of a double-precision number, the result is rounded to three decimal places. If the result is 24, the current arithmetic expression is eligible and is appended to D1 by D6.
After all loops are finished, if A7 finds no expression in D1, there is no solution.
View result in D1 when the program finishes execution:
![]()
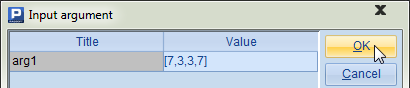
To change the random cards, we can change the arg1’s value to [7,3,3,7]:
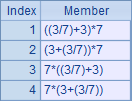
D1’s result when execution is finished:
We can call the previous program (24points.dfx) in another program to get the expressions whose result is 24 for all random four cards:
A |
B |
C |
|
1 |
=file(“d:/file/24points.dfx”) |
=create(Num1,Num2,Num3,Num4,Answer) |
|
2 |
13 |
=A2*A2 |
=B2*A2 |
3 |
=to(0,A2*C2-1).([~\C2+1, ~%C2\B2 +1,~%B2\A2+1,~%A2+1]) |
=A3.(~.sort()).id() |
>B3.run((a=~,B1.insert(0,a(1),a(2),a(3),a(4),call(A1,a)))) |
4 |
=file(“d:/file/24points.txt”) |
>A4.export@t(B1) |
In the above program, A3 lists all possible random 4 cards:
Since cards with same numbers get same result no matter what order they are arranged in, B3 sorts A3’s sequences and remove duplicates to reduce computations:
C3 calls 24points.dfx to calculate over each sequence in B3 and stores result in B1’s table sequence. Here’s B1’s final result:
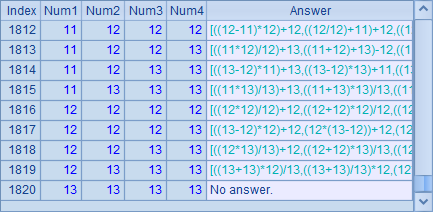
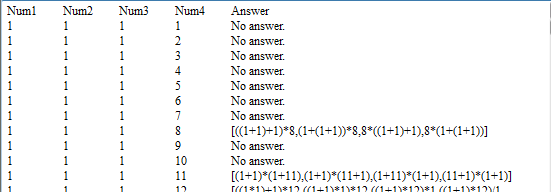
eProc supports exporting a result set to many types of files. Line 4 exports the final result to a target text file, 24points.txt, as shown below:
SPL Official Website 👉 https://www.scudata.com
SPL Feedback and Help 👉 https://www.reddit.com/r/esProcSPL
SPL Learning Material 👉 https://c.scudata.com
SPL Source Code and Package 👉 https://github.com/SPLWare/esProc
Discord 👉 https://discord.gg/2bkGwqTj
Youtube 👉 https://www.youtube.com/@esProc_SPL


