The sets in SPL are ordered, and members can be referenced by sequence numbers. Flexible use of sequence numbers can make the calculation simpler and more efficient.

1 Member access

Some functions of SPL can use serial number or serial number array as parameters. The simplest application is to access members directly with serial number, which is similar to arrays in general programming languages.

	A
1	[1,3,5,7,9]
2	=A1(1)
3	=A1(3)
4	>A1(2)=4
5	>A1(4)=8

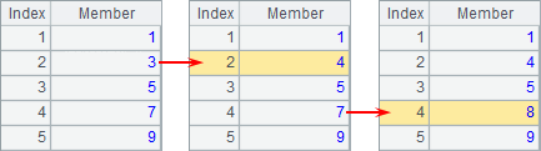
A2 and A3 get the members of the specified position from the sequence, and the position sequence number starts from 1, and the result is as follows:

 

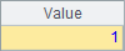
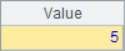
A4 and A5 modify a member of the sequence. In step-by-step execution, you can see the sequence changes in A1 as follows:

 

Using the A.m(i) function, you can get from the end or loop, which provides an effective supplement for A(i).

	A
1	[1,3,5,7,9]
2	=A1.m(3)
3	=A1.m(-2)
4	=A1.m@r(6)
5	=A1.m@r(12)
6	=A1.m(6)

A2 and A3 use the A.m() function to get the member value of the specified serial number from the sequence, where -2 represents the second member from the end. The code in A4 and A5 adds the @r option. When getting members, if the specified sequence number is out of bounds, it will be fetched circularly. For example, the member in A1 of sequence number 12 is looped twice, it is equivalent to getting the second member. The results of A2~A5 are as follows:

 

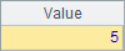
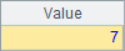
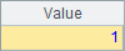
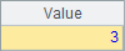
In A6, the specified sequence number 6 exceeds the length of the sequence and the @r option is not used, a null value will be returned.

 

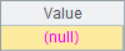
SPL also provides a set of functions for location finding, which start with p, such as:

	A
1	[3,5,1,9,7]
2	=A1.pos(5)
3	=A1.pmin()
4	=A1.pmax()
5	=A1.pselect(~%5==0)

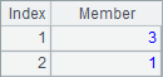
A2 finds the location sequence number of the specified member. If there are multiple members with the same value, only the first sequence number is returned. A3 and A4 return the sequence number of the minimum and maximum members, respectively. In A5, find the sequence number of the first member that meets the set conditions. Here, find the position of the first member of multiple 5. After calculation, the results of A2~A5 are as follows:

 

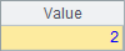
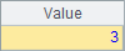
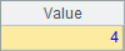
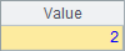
If the member cannot be found, the A.pos() function returns null, so you can use the A.pos() function to determine whether the member belongs to the set.

	A
1	[3,5,1,9,7]
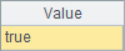
2	=A1.pos(1)!=null
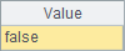
3	=A1.pos(2)!=null

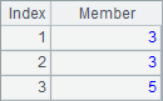
The calculation results of A2 and A3 are as follows:

 

2 Subset access

You can access a subset of a set by using sequence number array as parameters, such as:

	A
1	[3,5,4,6,1]
2	=A1([1,3,5])
3	=A1([3,5,2])
4	=A1([4,1,3,1])
5	>A1([1,3,5])=[12,43,28]
6	>A1([2,4,3])=0

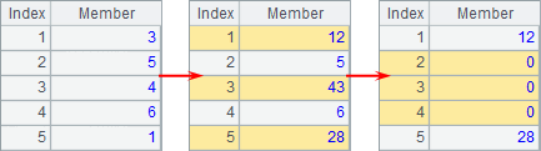
A2, A3 and A4 obtain subsets from the sequence respectively. After calculation, the results of A2, A3 and A4 are as follows: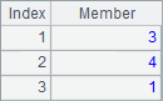

   

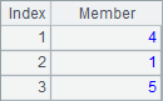
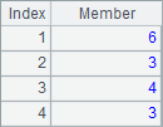
A5 and A6 modify the members in the sequence, and use sequence number array as parameters to modify multiple members at a time. During step-by-step execution, you can see the sequence changes in A1 as follows:

 

The A.m() function can also use sequence number array parameters to obtain subsets:

	A
1	[3,5,4,6,1]
2	=A1.m([1,-1])
3	=A1.m@r([1,6,12])
4	=A1.m@0([1,6,3])

In the example, you can use a negative number to represent counting backwards in the parameter array, or you can add the @r option to represent the position out of range rotation. In addition, you can use the @0 option. If there is an out of range sequence number in the parameter array, the corresponding null value will not appear in the result. The results of A2, A3 and A4 are as follows:

  

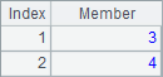
If you add the @a option to the location lookup function, you will find all the members that meet the conditions, and use their serial numbers to form a array to return:

	A
1	[3,2,1,9,6,9,1,2,8]
2	=A1.pos@a(2)
3	=A1.pmin@a()
4	=A1.pmax@a()
5	=A1.pselect@a(~%2==0)
6	=A1.pos@a(8)

Because @a option is added, A2 will return the position of all 2 in sequence A1, A3 will return the sequence number of all members with the minimum value, A4 will return the sequence number of all members with the maximum value, and A5 will return the sequence number of all members with multiple of 2. When using the @a option, even if only one member is found, the sequence of sequence number will be returned instead of the sequence number itself, such as A6 to find all the positions where 8 is located. The calculation results of A2 ~ A6 are as follows:

   

 

 

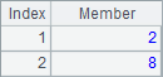
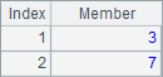
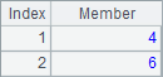
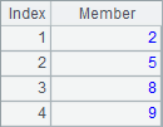
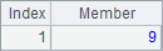
When it is necessary to use the A.pos()  function to return the positions of multiple members at the same time, you may need to add the @i option as needed, such as:

	A
1	[3,2,1,9,6,9,1,2,8]
2	=A1.pos@i([2,9,8])
3	=A1.pos@i([3,1,1,1])
4	=A1.pos@i([1,2,3])
5	=A1.pos([1,2,3])
6	=A1.pos([1,1,2,2])
7	=A1.pos([1,1,1,2,2,2,3,3])

When A.pos@i() is used to find the members in the parameter sequence, it will be one-way sequential; when only A.pos() is used, it will simply determine whether the sequence A contains each member in the parameter sequence. The results of A2~A7 are as follows:

 

 

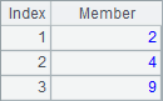
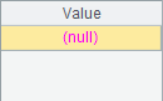
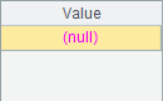
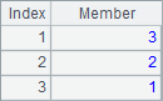
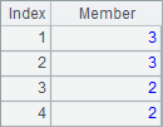
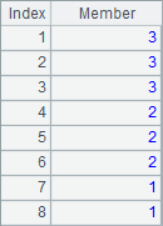
It can be seen that the results of A3 and A4 are null, in which the third 1 in the sequence cannot be found in A3 calculation, and 1,2,3 cannot be found in turn in A4 calculation. In other words, A.pos@i() will only return the increasing sequence, and if the result cannot be found, it will return null.

A.pos@i() will return null when a member cannot be found. However, due to the factors of order and repeatable members, it cannot be used to determine whether a subset is included. Generally, intersection operation is used:

	A
1	[3,2,1,9,6,9,1,2,8]
2	=A1.pos@i([1,9,6])==null
3	=A1.pos@i([1,2,3])==null
4	=A1.pos([1,2,3,4])==null
5	=A1.pos([1,2,3,3])==null
6	[1,1,2,2]
7	[1,1,2,2,3,3]
8	=A6^A1==A6
9	=A7^A1==A7

A2~A4 results are as follows：

 

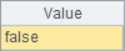
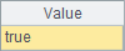
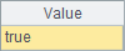
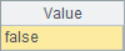
When using A.pos@i(B) to find and judge, if the result is not empty, it means that members in B can be found in A in turn, which means that A must contain B. But if the search result is null, it only means that members in B cannot be found in A in turn, and it does not mean that A must not contain B, for example, in A3.

When using A.pos(B) to find and judge, if the result is empty, it means that there must be members in B that cannot be found in A, which means that A must not contain B. However, if the search result is not empty, and if there are duplicate members in B, then there is no guarantee that A contains B, such as in A5.

The results of A8 and A9 are as follows：

 

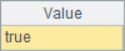
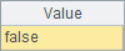
It is feasible to use B^A==B to judge whether A includes B. According to the results in A8 and A9, it can be determined that A1 contains A6, but A1 does not contain A7. When using this method, it should be noted that the operands of intersection operation cannot be reversed, otherwise, the order of members in the result of calculation A^B may be different from that of B, so it cannot be correctly judged.

3 Loop function positioning

Similar to the symbol ~, in the parameters of the loop function, you can use # to represent the sequence number of the current member.

	A
1	[5,4,3,2,1]
2	=A1.(#)
3	=A1.(#+~)
4	=A1.select(#%3==2)
5	=A1.group(int((#-1)/2))

A2 obtains the sequence composed of sequence number, A3 obtains the result sequence of adding each position member and sequence number. A4 use the A.select() function to select the second member of each three in the sequence of A1, that is, the second, fifth, eighth … member and form a sequence. A5 divides A1 into groups of every 2 members. The results of A2~A5 are as follows:

  

 

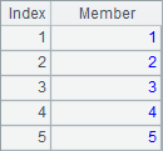
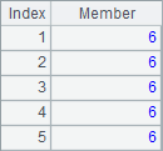
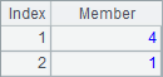
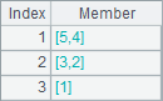
In loop function, SPL also provides access to members in a relative manner with the [ ] symbol:

	A
1	[1,2,3,4,5]
2	=A1.(~[0])
3	=A1.(~[1])
4	=A1.((~-~[-1])/~[-1])
5	=demo.query("select * from   STOCKRECORDS where STOCKID=000062").sort(DATE)
6	=A5.((CLOSING-CLOSING[-1])/CLOSING[-1])
7	0
8	=A5.max(if(CLOSING>CLOSING[-1],A7=A7+1,A7=0))

A2 is to take out each member itself from the sequence. A3 takes the next member from each position. A4 calculates the growth rate of each member in the sequence compared with the previous member. A2, A3 and A4 are calculated as follows:

   

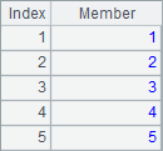
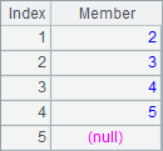
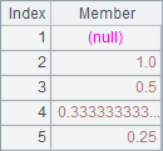
A5 query the stock information of the specified number. A6 calculates the daily share price increase, A8 further calculates the maximum consecutive rising days of this stock. The results of A6 and A8 are as follows:

 

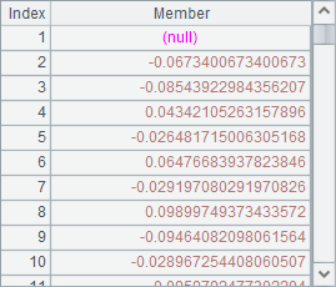
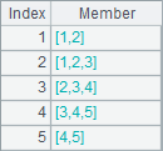
You can also use ~[a, b] to access subsets in loop operations:

	A
1	[1,2,3,4,5]
2	=A1.(~[-1,1])
3	=A1.(~[-1,1].avg())
4	=A1.(~[1-#,0].sum())
5	=A1.(~[,0].sum())
6	=A1.(~[0,].sum())

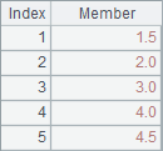
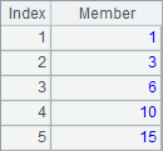
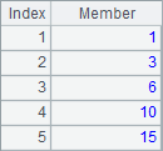
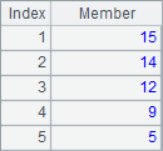
A2 lists the three members for each position in the sequence. A3 calculate the moving average of each position. A4 and A5 are both cumulative summations. A6 calculates the reverse cumulative sum, which is the sum of the remaining members. The results of A2~A6 are as follows:

 

 

4 Aligned access

As we know, the symbol # in a loop function is used to represent the serial number of the current member. In fact, it is a number, which can participate in operations like other numbers, especially can be used as a serial number to access members of other sequences. With this feature, we can access other sequences in alignment in the calculation:

	A
1	[1,2,3,4,5]
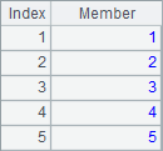
2	=A1.(A1(#))
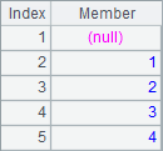
3	=A1.(A1.m(#-1))
4	[5,4,3,2,1]
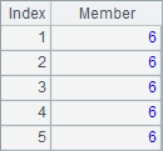
5	=A1.(~+A4(#))
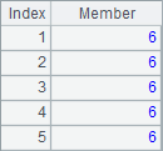
6	=A1++A4
7	=10.(if(#%2==1,A1((#-1)/2+1),A4(#/2)))

In the loop calculation, the # in the expression can be used to represent the current sequence number. After calculation, the results of A2, A3, A5, A6 and A7 are as follows:

     

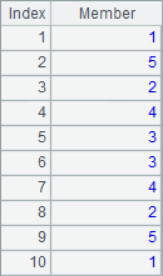
When multiple equal length sequences are used, the effect of similar record fields can be achieved by using the aligned access:

	A
1	[Bray,Jacob,Michael,John]
2	[65,87,98,72]
3	[76,82,78,88]
4	=A1.ranks@z(A2(#)+A3(#))
5	=A1.new(~:name,A4(#):rank)

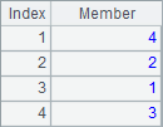
A4 calculate the ranking of the total score, and get the scores according to the position when calculating the total score. A5 generates the sequence table of names and rankings, and also associates the data in the two sequences according to their positions. A4 and A5 results are as follows:

   

 

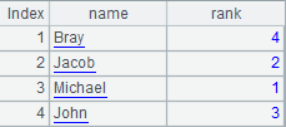
5 Sequence alignment

Before using aligned access, it is necessary to ensure that all sequences have been arranged in the same order, but in practice, the sequences may not always be like this. In this case, use the alignment function A.align() to reorder the sequence according to a benchmark sequence:

	A	B
1	=demo.query("select * from   EMPLOYEE")	/Employee table
2	=demo.query("select * from   ATTENDANCE").align(A1:EID, EMPLOYEEID)	/ Align the attendance table by employee ID
3	=demo.query("select * from PERFORMANCE").align(A1:   EID, EMPLOYEEID)	/ Align the performance table by employee ID
4	=A1.new(NAME,SALARY*(1+A2(#). ABSENCE+A3(#). EVALUATION):salaryPaid)	/Create a new sequence table to calculate salary. A1,A2, and A3 are in same order.
5	=demo.query("select * from GYMSCORE   where EVENT='Vault'")	/ Vault score
6	=demo.query("select * from GYMSCORE   where EVENT='Floor'").align(A5:NAME,NAME)	/Floor score，aligned by athlete
7	=A5.(round(SCORE*0.6+A6(#).SCORE *0.4,3))	/ Calculate weighted score
8	=A7.ranks@z()	/ Calculate weighted ranking
9	=A5.new(NAME,A7(#):score,A8(#):rank)	/Create new sequence table to calculate athlete’s weighted score and ranking

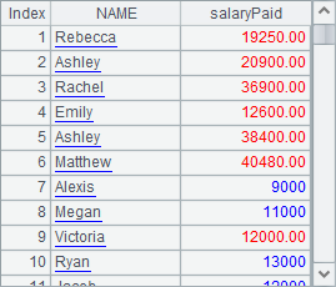
The sequence tables of A2 and A3 have been aligned according to the employee ID in A1, and A4 calculates the salary sequence table of employees as follows:

 

A6 aligns the data with the names of the athletes in the A5 sequence table, and A7 calculates the weighted scores accordingly. A8 calculates the ranking of weighted scores, and finally A9 sorts out the result sequence table as follows:

 

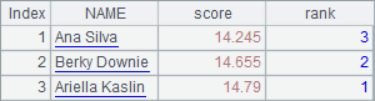
In fact, the alignment function using the @a option will also return a sequence aligned with the base sequence, except that each member of the sequence is a set, which can also be applied to aligned access.

	A	B
1	=demo.query("select * from   EMPLOYEE")	/Employee table
2	[California,Texas,Pennsylvania]
3	=A1.align@a(A2,STATE)	/Aligned grouping by states in A2
4	=A3.new(A2(#):STATE,~.count(): Count,round(~.avg(age (BIRTHDAY)),2):Age)	/ Use # to find the field value in A2 according to the serial number in A3

After calculation, A4 result is as follows：

 

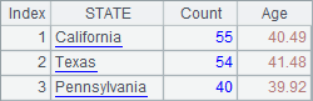
A.align() function without option will take out the first member from the source sequence for each member of the corresponding reference sequence to form a set and return, instead of returning the set of sets. When it is clear in advance that each grouping subset has only one member, using A.align() function is equivalent to completing an operation of sorting by reference sequence.

 Similarly, enumeration groups can also be accessed by alignment, but the @1 option in A.enum() is invalid, and only the grouping problem can be handled:

	A
1	=demo.query("select * from   EMPLOYEE")
2	[AgeGroup1,AgeGroup2,AgeGroup3]
3	[?<=35,?>35 &&   ?<=40,?>40]
4	=A1.enum(A3,age(BIRTHDAY))
5	=A4.new(A2(#):AgeInterval,~.count():Count)

A5 calculates the total number of employees in the three age groups as follows:

 

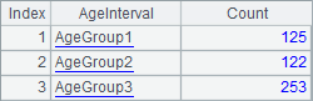
6 Interval array

Array is a special set. It is a set, and can apply various set operations. At the same time, it can be used as a sequence number to access the subset of other sequences. Flexible use of array is an important part of establishing sequence number thinking, such as:

	A
1	=to(10)
2	=to(3,8)
3	=A1.step(3,2)
4	=20.step(4,2,3)

The to()function can get a sequence of consecutive integers, while the step() function can set parameters such as the interval of the members of the sequence. The A1-A4 results are as follows:

  

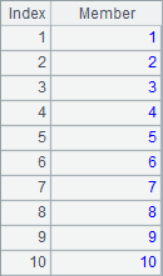
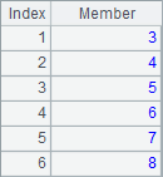
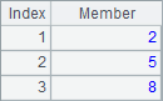
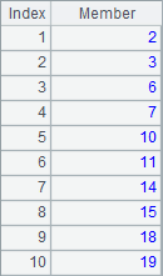
The position sequence of a subsequence in the original sequence can be used to process subsets, such as:

	A	B
1	=to(100)		/A sequence of 1 to 100
2	=A1(100.step(14,7))=0		/ From 14 onwards, multiples of 7 are assigned to 0
3	=A1.run(if(~>1,A1(100.step(~,~+~ ))=0,0))
4	=A1.select(~>1)		/ Generate prime table: assign 0 to positions that are composite numbers, leaving only the prime
5	=100.(rand())		/ Generate 100 random numbers
6	=A5(to(50))
7	=A5(to(51,100))
8	>A5(100.step(2,1))=A6
9	>A5(100.step(2,2))=A7		/ Shuffle A5, alternating the first 50 and the last 50

In the above example, you can use an array to assign values to the original sequence, or you can obtain subsequences, etc.

7 Ordinal sequence

If we sort the sequence, we will lose the original sequence information of the members, but sometimes this information needs to be used. For example, we want to know the entry sequence of the oldest three employees in the whole company, and the rise of the stock price in the highest three trading days.            

For this purpose, SPL provides A.psort() function to return the original sequence number of members after sorting.

	A
1	[c,b,a,d]
2	=A1.psort()
3	=A1(A2)
4	=A1.sort()
5	=A3==A4

A2~A5 results are as follows：

  

 

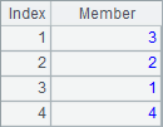
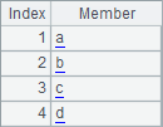
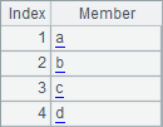
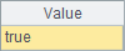
Generally speaking, in the sequence returned by A.psort(), the first number is the sequence number of the member in the original sequence that should be ranked in the first place in the current ranking, and the second number is the sequence number of the member in the original sequence that should be ranked in the second place in the current ranking,...

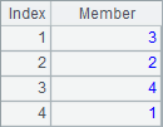
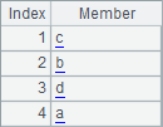
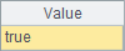
For the sequence generated by ordinal sequence, you can also use A.inv() function to obtain the inverse sequence of ordinal sequence for recovery operation, such as:

	A
1	[c,b,d,a]
2	=A1.sort()
3	=A1.psort().inv()
4	=A2(A3)
5	=A4==A1

A2~A5 results are as follows：

 

 

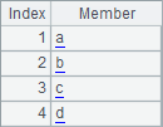
With two functions A.psort() and A.inv(), you can easily solve the problem of maintaining the original sequence number:

 

	A	B
1	=demo.query("select * from EMPLOYEE  ").sort(HIREDATE)
2	=A1.psort(BIRTHDAY:-1)	/ Returns the ordinal sequence of A1 sorted by birthday
3	=A2(to(3))	/Ordinal sequence of A1 of minimum 3 birthday values
4	=demo.query("select * from   STOCKRECORDS where STOCKID=000062").sort(DATE)
5	=A4.psort(CLOSING:-1)	/ Ordinal sequence of A4 sorted in descending order of closing price
6	=A5(to(3))	/ The sequence number of records in A4 with the highest closing price for 3 days
7	=A6.(A4(~).CLOSING/A4.m@0(~-1).CLOSING-1)	/ The increase of these three days. It shall be calculated in the order of A4
8	=A6.(A4.calc(~,(CLOSING-CLOSING[-1])/CLOSING[-1]))	/ The calc function can be used to abbreviate the expression in A7

 

In data searching, dichotomy can greatly improve the efficiency, but this method requires the original sequence to be orderly for the keywords to be searched, if the original sequence is out of order, it needs to be sorted first. If you want to find the member itself, there is no problem in sorting first, but when you want to find the member's serial number, sorting will destroy this information. At this time, you need to use the A.psort() function, such as:

	A	B
1	=demo.query("select * from EMPLOYEE  ").sort(HIREDATE)
2	=A1.psort(NAME)	/The ordinal sequence of A1 sorted by nameA1
3	=A1(A2)	/Sequence sorted by name
4	=A3.pselect@b(NAME:"David")	Find David's serial number in A3 by dichotomy
5	=A2(A4)	/ David's serial number in A1

Here, using A.psort() is equivalent to building a binary search index for a sequence. A sequence can build multiple search indexes according to different keywords at the same time.

The alignment grouping function can also return the array composed of sequence numbers without directly returning the aligned sequence, such as:

	A	B
1	=demo.query("select * from   SALES").sort(AMOUNT:-1)	/Sort the orders by descending amount
2	[QUICK,ERNSH,HANAR,SAVEA]
3	=A1.align@1p(A2,CLIENT)	/ Alignment grouping by client sequence in A2 and return the sequence number
4	=A3.new(A2(#):NAME,A1(~).AMOUNT:   Amount,~:Rank)	/ Use the sequence number in A3 to find the order amount and total amount ranking in A1

8 Location calculation

After calculating the sequence number of the required record, you can use positioning calculation A.calc() to calculate the required result. Using location calculation can avoid unnecessary calculation and improve the calculation efficiency.

	A
1	=file("VoteRecord")
2	=A1.import@b()
3	[Califonia,Ohio,Illinois]
4	=A2.pselect@a(A3.pos(State)>0)
5	=A2.calc(A4,Votes[-1]-Votes+1)

The calculation results in A2, A4 and A5 are as follows：

 

  

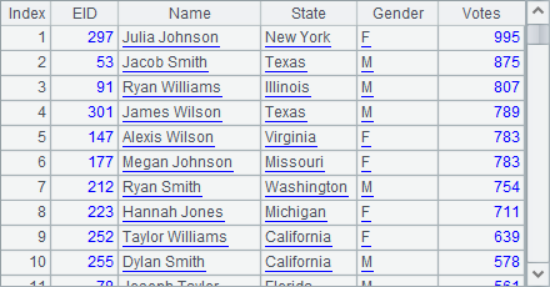
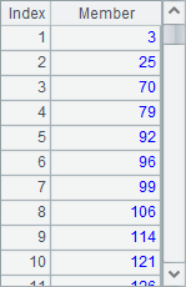
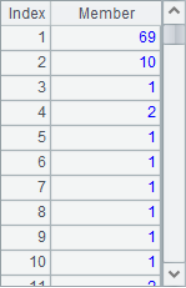
In this example, the binary file VoteRecord stores the results of a poll and has been sorted in descending order. A4 calculates the employee ordinal sequence for the designated state. According to the ordinal sequence, A5 calculates how many tickets these employees need to get to make the ranking rise. For example, Ryan Williams, who is currently ranked No. 3, needs to get another 69 votes to advance 1. Cross row processing is required in the calculation, which can not only be completed according to the data of the selected employees, but also needs the relevant data in the original table.