Below are order table, whose primary key is id, and order_detail table, which has a composite primary key consisting of id and productid. We might want to perform joins on the two tables. Suppose we are trying to group data by customer and order date and subtotal order amounts in each group. The grouping fields are order table’s customerid and orderdate, and order amount is the result of multiplying price by quantity in the order_detail table.

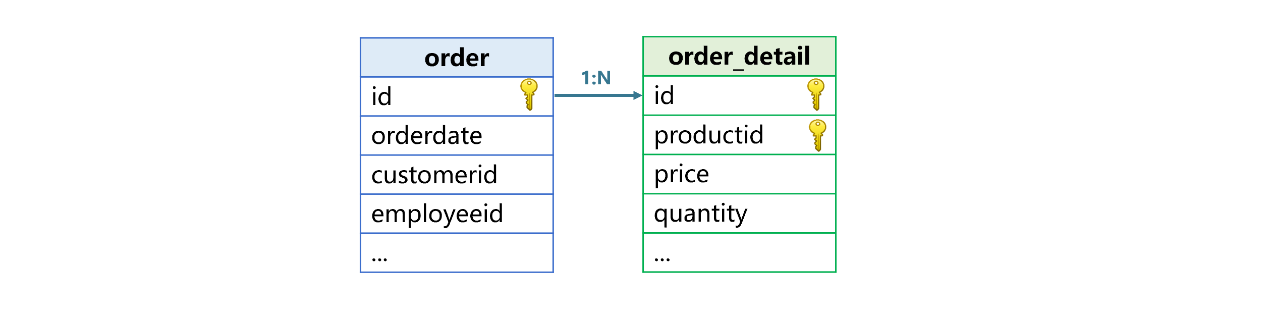
Such a join is rather common. Characteristics are: The join field(s) is the primary key or one or more fields of a composite key; relationship between tables is one-to-one or one-to-many. Two tables with a one-to-many relationship are the primary table and the sub table; a primary table can have more than one sub table.

This join is referred to as JOIN in SQL. Databases use HASH JOIN algorithm to handle it. When both tables to be joined are huge, the computing speed will be unbearably slow. This is because the algorithm is, in essence, an in-memory one. It will divide data into heaps and buffer them one by one to convert the JOIN on two large data sets to JOINs between smaller data sets. This involves high I/O cost, and if the HASH function is not rightly selected, needs more rounds of buffering. Moreover, the HASH heaping technique is difficult to implement with parallel processing, and even if it is successfully implemented, the execution of parallel threads will bring about shared resource collision and heavy memory usage, considerably compromising the performance of parallel processing.

But, if we can store the two to-be-joined tables according to the orders of their primary keys in the first place, we are able to use the merge algorithm to achieve the join. The order-based merge algorithm only traverses both tables in order without the need of hard disk buffer, reducing IO cost greatly. Its complexity is linear while the HASH JOIN has a quadratic complexity. As the complexity reduces strikingly, performance leaps up.

Sorting is costly. Frequent sorting actions weaken the overall performance below that of the HASH JOIN algorithm. The good news is that such joins that are based on the primary key or one or more fields of a composite key instead of any other field(s), like the order table vs order_detail table, are prevalent. So, the order-based merge algorithm is widely applicable with its ability of handling computing scenarios involving the key-based joins. A presorting by the primary key is slow though, it is a matter of a one-off action and uses the key-based storage alone without any redundant data.

It is easy to achieve segment-based parallel processing with the order-based merge algorithm. Dividing one table into segments for parallel processing is simple, but segmenting two associative tables must be synchronous, otherwise records in the two tables will become mismatched at merge. Tables ordered by the join field(s) can ensure synchronous partition of two tables being aligned with each other, giving full play to the advantages of parallel processing.

The SQL language defines all JOIN operations using the Cartesian product of two tables and does not distinguish different types of joins according to whether the join fields are primary keys, foreign keys or other combinations. By not postulating that, for some JOINs, tables are associated through primary keys (or one or more primary-key elements), SQL cannot design algorithms primary-key-based algorithms but only rely on engineering optimization. Some databases will check whether the involved data tables are physically ordered by related fields at storage, and adopt the merge algorithm if they are. However, relational databases, which are based on the concept of unordered sets, are naturally unable to ensure the physical orderliness, but instead many actions can even undermine the favorable conditions for achieving the merge algorithm. Using an index can achieve the logical orderliness, but the physically unordered data will still reduce the efficiency of traversal.

A better alternative is the open-source esProc SPL. It supports the order-based merge algorithm to implement the join between order table and order_detail table. The code is as follows:

1.  Sort the two tables to be joined by the primary key so that they are physically stored in order.

A1=file("order_original.ctx").cursor().sortx(id)    // Perform external storagesorting on the original order table by primary key (id)

A2=file("order_detail_original.ctx").cursor().sortx(id,productid)

       // Perform external storage sorting on the original order_detail table by primary key (id and productid)

>file("order.ctx").create(#id,…).append(A1)

    // Create a new order table ordered by primary key and append order data to it

>file("order_detail.ctx").create(#id,#productid…).append(A2)

    // Create a new order_detail table ordered by primary key and append order details data to it

2.  Perform order-based merge algorithm

A1=file("order.ctx").open().cursor@m(id,customerid,employeeid,orderdate)

    // Generate a multicursor based on the new order table and retrieve data from it using parallel threads

A2=file("order_detail.ctx").open().cursor(id,productid,price,quantity;;A1)

    // Generate a multicursor being aligned with A1 for the new order_detail table; the synchronous partition ensure correct id matching between two cursors

A3=joinx(A1:id,o;A2:id,od)

    // Merge the two ordered cursors by id fields

…   // Perform further computations

Tests show that, under the same hardware environment and without the use of efficient columnar storage, SPL is several to dozens of times faster than Oracle in joining a huge order table and a huge order_detail table.

Find more comparisons in Performance Optimization Skill: Order-based MERGE.