"We can invoke a function recursively to solve the Tower of Hanoi problem. The Tower of Hanoi pro .."

mars RaqForum 25 No.
283 View • 1 Years ago

11.12 Recursion: Tower of Hanoi problem

We can invoke a function recursively to solve the Tower of Hanoi problem.
The Tower of Hanoi problem is a typical recursion scenario. The problem aims to move the entire stack of disks on rod A to rod C with the original order retained, where moves are allowed only if one disk is moved at a time and if they place smaller disks on top of larger disks.

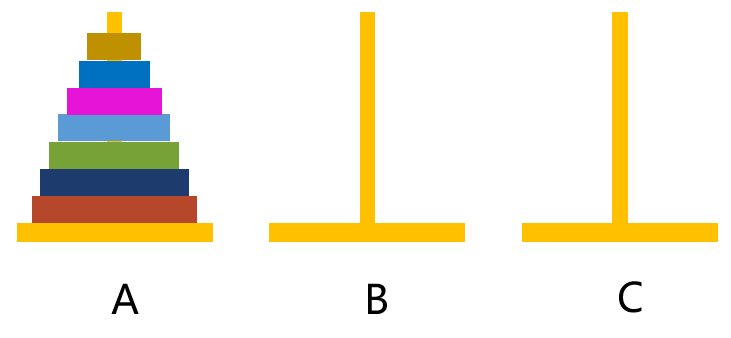
imagepng

Disks are named 1- n from small to big. During the whole process we will always treat the n disks as two groups – the nth disk and the n-1 disks. We move n-1 disks to rod B and the nth disk to rod C, and then put n-1 disks to rod C.
SPL provides func(c,…) function to perform a recursive operation.

SPL script:

	A	B	C
1	func
2		if(A1==1)	>output("move disk" + string(A1) + "from" + B1 + "to" + D1)
3		else	>func(A1,A1-1,B1,D1,C1)
4			>output("move disk" + string(A1) + "from" + B1 + "to" + D1)
5			>func(A1,A1-1,C1,B1,D1)
6	>func(A1,5,“A”,“B”,“C”)

A1 Define a function.
B2-C2 Move the disk to rod C when there is only one disk.
C3 Move the n-1 disks on rod A to rod B.
C4 Move the bottom disk on rod A to rod C.
C5 Move the n-1 disks on rod B to rod A.
A6 Four function parameters – number of disks (name), original tower, intermediate tower and target tower.

When there are 5 disks on rod A, the output result is as follows:

imagepng