...

Least-squares algorithm linear fitting

 

The steps of least squares fitting are:

Given a set of data points(x1,y1)，(x2,y2)……(xm,ym)

（1）Determine the type of curve to be used to fit the data, for example ..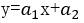

（2）Substitute the data points into the curve and get the system AX=Y

（3）Solve AX=Y using linefit() linear least square method

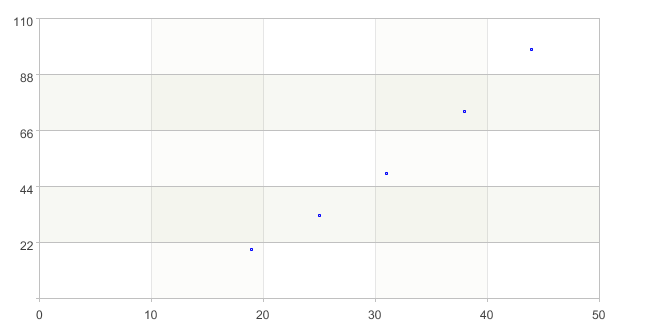
For example, the data in the following table is fitted with the least square method

x

19

25

31

38

44

y

19

32.3

49

73.3

97.8

SPL code：

A

1

[19,25,31,38,44]

2

[19,32.3,49,73.3,97.8]

3

=canvas()

4

=A3.plot("NumericAxis","name":"x")

5

=A3.plot("NumericAxis","name":"y","location":2)

6

=A3.plot("Dot","lineWeight":0,"lineColor":-16776961,"markerWeight":1,"axis1":"x","data1":A1,"axis2":"y","data2": A2)

7

=A3.draw(800,400)

8

[[19,1],[25,1],[31,1],[38,1],[44,1]]

9

=linefit(A8,A2).conj()

10

=to(10,50)

11

=A10.([~,A9(1)*~+A9(2)])

12

=A3.plot("Line","markerStyle":0,"axis1":"x","data1":A11.(~(1)),"axis2":"y", "data2":A11.(~(2)))

13

=A3.draw(800,400)

A1-A7 Import the data, draw the scatter plot, and determine the curve type

A3 Generate canvas

A4 Draw horizontal axis "x"

A5 Draw the vertical axis "y"

A6 Plot point primitives. The X-axis data is A1, and the Y-axis data is A2

A7 The distribution of observation points is linear, and the type of fitting curve is selected as ..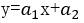

..

A8-A9 Take the data points into the curve and write them in matrix form, get

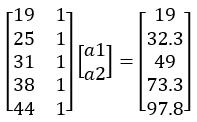.., as the AX=Y form

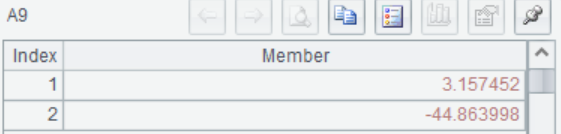
Pass the matrix parameters into linefit(A,Y) and the value of a1, a2 are solved, a1 =3.157452，a2=-44.8639981

..

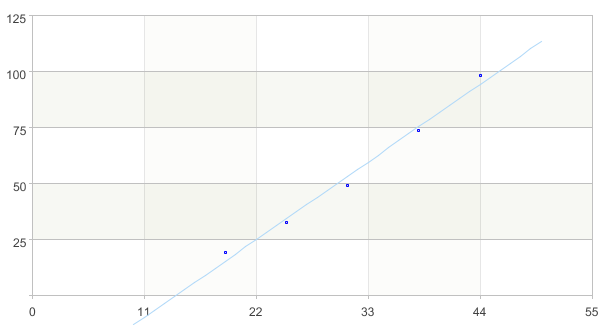
A10-A13 Draw the fitted curve onto the scatter plot for intuitive comparison

..

There are many types of curves that can be fitted using linear least square method linefit(). Common ones are:

（1） Line ..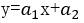

（2） Polynomial ..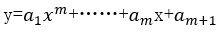

（3） Hyperbola ..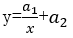

（4） Exponential curve ..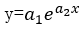

For hyperbolic and exponential curves, variable substitution is required to transform them into linear functions of a1 and a2


 
 •  151 View  •