SPL Programming Exercise - Chapter 3 Doing loop
3.1 Single layer loop
1. Enter a positive integer n and output 1, 2, 3… n-1, n
2. Calculate the sum of 2+4+6+…+100
3. Enter a positive integer n and calculate the factorial of n
4. Calculate the sum of all odd and even numbers in 1,2,3,…,100?
5. Write a program that outputs the number between 1 and 100 where the product of each digit is greater than the sum of each digit
6. Please print out all three-digit narcissus numbers?
Tip:
(1) The narcissus number refers to an n-digit number (n ≥ 3), where the sum of the n-th powers of each digit is equal to itself. (For example: 13 + 53+ 3^3 = 153)
(2) for a,b, indicating that the loop variable will change from a to b
7. Sum and find the value of s=a+aa+aaa+…+aa… a (where the number of a in the last number is n), where a is a number from 1 to 9, for example: 2+22+222+2222+22222 (where a=2 n=5)
Input: One line consisting of two integers, the first being a and the second being n (1 ≤ a ≤ 9, 1 ≤ n ≤ 9), separated by a comma.
Output: One line, the value of s.
Input example: 2,5 corresponds to output: 24690
8. Enter a positive integer greater than 1 and determine if it is a prime number. If it is a prime number, output Yes; If it is not a prime number, output the number of its factors
Tip 1: Prime numbers refer to natural numbers that have no other factors than 1 and itself among natural numbers greater than 1
Tip 2: Factor refers to the factor of a if the quotient of integer a divided by integer b (b ≠ 0) is exactly an integer without a remainder, then b is the factor of a
9. Calculate the series: S=1+1/3+1/5+1/7+… sum of the first 100 terms
10. Programming to calculate the expression 
3.2 Multilayer loop
1. Find the factor of each number between 2 and 50
2. Calculate the area of a circle with a radius from 1 to 10 and the area less than 100
3. Write a program to print the following graphics
Tip: Use output()and output@s () to control whether to add or not to add a carriage return
*********
********
*******
******
*****
****
***
**
*
4. Write a program to print the following diamond patterns. The number of rows in a diamond can be entered, and the size of the diamond varies depending on the number of rows.

5. Write a program using the for and break statements to determine whether any positive integer greater than 1 is a prime number. If it’s, outputting Yes, not outputting No
6. Find all prime numbers between 100 and 200
7. If a number is exactly equal to the sum of its factors, it is called a “perfect number”. For example, 6=1+2+3. Programming to find all perfect numbers within 1000
8. There are several balls in red, yellow, blue, white, and black colors in the pocket. Take out three balls of different colors from your pocket each time and ask how many ways to take them.
(1) The three balls are in order, with red, yellow, blue and blue, yellow, and red being different ways of picking them up
(2) 3 balls without order, red, yellow, blue, and blue, yellow, and red are the same selection method
3.3 Conditional loop
1. Enter a positive integer and output it in reverse order. For example, if input 12345, output 54321
2. Enter a positive integer and check if it is a symmetric number (palindrome). If it is output Yes; If it’s not output No
Tip: Symmetric numbers refer to numbers that are reversed to be the same as the original number. For example, 12321 is a symmetric number and 12345 is not a symmetric number
3. Enter a positive integer, take out each odd digit in the positive integer in sequence, and then arrange the extracted numbers in the original order to form a new positive integer and output it
Tip: If the original number is 1215348, the new number formed is 1153
4. Output prime numbers up to 1000
5. Each rooster is worth 5 dollar, each hen is worth 3 dollar, and three chicks are worth 1 dollar. Buy 100 chickens for 100 dollar and ask: How many roosters, hens, and chicks are there in these 100 chickens?
6. What is the output result of the following program?
| A | B | C | D | |
|---|---|---|---|---|
| 1 | for 5 | |||
| 2 | for 2 | |||
| 3 | if A1==2 | next A1 | ||
| 4 | if A1==4 | break A1 | ||
| 5 | >output(A1) |
3.4 Endless loop
1. Calculate the area of the circle, with radius values of 1, 2, 3, … until the area value exceeds 1000.
2. Write the program using an endless loop, calculate the approximate value using the formula 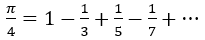 , until the absolute value of the last term is not greater than
, until the absolute value of the last term is not greater than 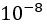 .
.
3. Using Taylor’s formula 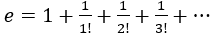 , calculate the approximate value of the natural logarithm base e until the absolute value of the last term is not greater than
, calculate the approximate value of the natural logarithm base e until the absolute value of the last term is not greater than 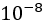 .
.
Suggestedanswers:
3.1 Single layer loop
1.
| A | B | |
|---|---|---|
| 1 | 100 | |
| 2 | for A1 | >output(A2) |
2.
| A | B | |
|---|---|---|
| 1 | =0 | |
| 2 | for 50 | >A1+=2*A2 |
Store the calculation result in A1
3.
| A | B | |
|---|---|---|
| 1 | 10 | 1 |
| 2 | for A1 | >B1=B1*A2 |
Store the calculation result in B1
4.
| A | B | C | |
|---|---|---|---|
| 1 | 0 | 0 | |
| 2 | for 100 | if A2%2!=0 | >A1+=A2 |
| 3 | else | >B1+=A2 |
A1 Odd Sum
B1 even sum
5.
| A | B | C | |
|---|---|---|---|
| 1 | for 100 | =A1%10 | |
| 2 | =A1\10 | ||
| 3 | if B1*B2>B1+B2 | >output(A1) |
6.
| A | B | C | |
|---|---|---|---|
| 1 | for 100,999 | =A1\100 | /The hundreds digit |
| 2 | =A1\10%10 | /The tens digit | |
| 3 | =A1%10 | /Single digit | |
| 4 | if B1*B1*B1+ B2*B2*B2+ B3*B3*B3==A1 | >output(A1) |
7.
| A | B | |
|---|---|---|
| 1 | 2 | 5 |
| 2 | 0 | 0 |
| 3 | for B1 | >A2=A2+A1 |
| 4 | >B2=B2+A2 | |
| 5 | >A1=A1*10 |
A2 The value to be added for each loop, such as 22222
B2 Sum Result
8.
| A | B | C | |
|---|---|---|---|
| 1 | 97 | 0 | |
| 2 | for A1 | if A1%A2==0 | >B1+=1 |
| 3 | =if(B1==2,output(“Yes”),output(B1)) |
9.
| A | B | |
|---|---|---|
| 1 | 0 | |
| 2 | for 100 | >A1+=1/(2*A2-1) |
10.
| A | B | |
|---|---|---|
| 1 | 100 | |
| 2 | for A1 | >B1+=A2*A2 |
| 3 | >B1=1/A1*B1 |
A1 Input the value of n
B1 Save calculation results
3.2 Multilayer loop
1.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | for 2,50 | >output(“Factors of”/A1/“:”) | ||
| 2 | for A1 | if A1%B2==0 | >output(B2) |
2.
| A | B | C | |
|---|---|---|---|
| 1 | for 1,10 | =3.14*A1*A1 | |
| 2 | if B1>100 | break | |
| 3 | >output(A1,B1) | ||
| 4 | >output(“When r=”/A1/“, S>100”) |
3.
| A | B | C | |
|---|---|---|---|
| 1 | 9 | ||
| 2 | for A1 | for A1+1-A2 | >output@s(“*”) |
| 3 | >output("") |
4.
| A | B | C | |
|---|---|---|---|
| 1 | 9 | ||
| 2 | for A1\2+1 | for A1\2+1-A2 | >output@s(" ") |
| 3 | for 2A2-1>output@s("") | ||
| 4 | for A1\2+1-A2 | >output@s(" ") | |
| 5 | >output("") | ||
| 6 | for A1\2 | for A6 | >output@s(" ") |
| 7 | for A1-2A6>output@s("") | ||
| 8 | for A6 | >output@s(" ") | |
| 9 | >output("") |
5.
| A | B | C | |
|---|---|---|---|
| 1 | 173 | ||
| 2 | for 2,A1-1 | if A1%A2==0 | break |
| 3 | =if(A2==A1,output(“Yes”),output(“No”)) |
6.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | for 100,200 | |||
| 2 | for 2,A1-1 | if A1%B2==0 | break | |
| 3 | =if(B2==A1,output(A1)) |
7.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | |||
| 2 | for 1000 | |||
| 3 | for A2-1 | if A2%B3==0 | >A1+=B3 | |
| 4 | if A1==A2 | >output(A2) | ||
| 5 | >A1=0 |
8.
(1)
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 0 | |||||
| 2 | for 5 | |||||
| 3 | for 5 | if B3!=A2 | ||||
| 4 | for 5 | if D4!=B3 && D4!=A2 | >A1+=1 |
The calculation results are saved in A1, with 60 different selecting methods.
(2)
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | |||
| 2 | for 5 | |||
| 3 | for A2-1 | |||
| 4 | for B3-1 | >A1+=1 |
The calculation results are saved in A1, with 10 different selecting methods.
3.3 Conditional loop
1.
| A | B | |
|---|---|---|
| 1 | 12345 | |
| 2 | for A1!=0 | >B1=B1*10+A1%10 |
| 3 | >A1=A1\10 |
B1 stores output result
2.
| A | B | |
|---|---|---|
| 1 | 12321 | |
| 2 | =A1 | |
| 3 | for A2!=0 | >B1=B1*10+A2%10 |
| 4 | >A2=A2\10 | |
| 5 | =if(A1==B1,output(“Yes”),output(“No”)) |
3.
| A | B | C | |
|---|---|---|---|
| 1 | 1215348 | ||
| 2 | 1 | ||
| 3 | for A1!=0 | =A1%10 | |
| 4 | if B3%2!=0 | >B1=B1+B3*A2 | |
| 5 | >A2=A2*10 | ||
| 6 | >A1=A1\10 |
B1 stores output results
A2 is used to store the digits after each loop
4.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | for 1000 | if A1==2 | >output(A1) | |
| 2 | for 2, A1-1 | if A1%B2==0 | next A1 | |
| 3 | >output(A1) |
5.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | for 100 | if 5*A1>100 | break | |
| 2 | for 100-A1 | =100-A1-B2 | =5*A1+3*B2+C2/3 | |
| 3 | if D2>100 | next A1 | ||
| 4 | else if D2<100 | next | ||
| 5 | >output(A1,B2,C2) |
In the code, A1 loops through the total number of roosters; In B1, if the total price of the roosters has exceeded 100, it indicates that there are too many roosters in total. At this point, in C1, use the break command to terminate the loop. B2 loops through the possible number of hens. In D3, if it is found that the total price of the current chickens has exceeded 100, it indicates that there are already too many hens in the current total. Next A1 can be used to increase the total number of roosters and try again. In D4, the total price of the current chickens is still less than 100. You can continue to increase the total number of hens to try. The next command here will skip the current innermost loop code, which is the loop with B2 as the main cell.
3.4 Endless loop
1.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | |||
| 2 | for | =3.14*A1*A1 | if B2>1000 | break |
| 3 | >output(A1,B2) | |||
| 4 | >A1+=1 |
2.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 1 | ||
| 2 | for | =A1/B1 | if abs(B2)<=number(“1E-8”) | break |
| 3 | >C1+=B2 | |||
| 4 | >A1*=-1 | |||
| 5 | >B1+=2 | |||
| 6 | >output(4*C1) |
3.
| A | B | C | |
|---|---|---|---|
| 1 | =1 | =1 | 1 |
| 2 | for | >C1=C1*B1 | |
| 3 | if 1/C1<=number(“1E-8”) | break | |
| 4 | >A1=A1+1/C1 | ||
| 5 | >B1+=1 | ||
| 6 | >output(A1) |
SPL Official Website 👉 https://www.scudata.com
SPL Feedback and Help 👉 https://www.reddit.com/r/esProc_SPL
SPL Learning Material 👉 https://c.scudata.com
SPL Source Code and Package 👉 https://github.com/SPLWare/esProc
Discord 👉 https://discord.gg/cFTcUNs7
Youtube 👉 https://www.youtube.com/@esProc_SPL



Chinese version