The following is part of the data from the simplified user behavior table actions, which records the occurrence time of 9 types of events for each user:

Download test data

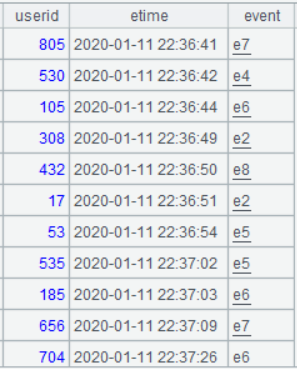
1.Find users whohave sequentially triggered events e2, e3, e7

Sequential events do not require continuity.

First, group the events by user. Then, sort each user’s events by time. Next, loop through each user’s e2 event to search for an e3 event after it. If an e3 is found, search for an e7 event after e3. If an e7 is found, the user is deemed to satisfy the criteria.

Let’s look at the SQL code first:

select distinct t1.userid 
from actions t1 join actions t2 join actions t3 
    on t1.userid=t2.userid and t2.userid=t3.userid 
        and t1.etime<t2.etime and t2.etime<t3.etime
where t1.event='e2' and t2.event='e3' and t3.event='e7';

SQL can’t keep grouped subsets, making it impossible to write processing statements targeting individual users after grouping, and implementing loop-based conditional logic is also very difficult. Therefore, self-joins have to be used here to filter sequential events using join conditions.

The conditions are scattered across the ON and WHERE clauses, and in fact, they could be written in either clause. It just depends on how you understand filtering and joining. This implementation approach is unnatural.

SPL can keep grouped subsets for further computation; looping is also easy, but not needed here. In addition, SPL has powerful ordered set operation capabilities, and its pos function can find subsequences from a sequence, thus making it easy to write code that fits natural logic.

	A
1	="e2,e3,e7".split@c()
2	=file("actions.txt").import@t().sort(etime)
3	=A2.group(userid)
4	=A3.select(~.(event).pos@i(A1)).(userid)

A2: Load the data and sort it by etime.

SPL IDE is highly interactive, enabling step-by-step execution and easy visual inspection of the results of each step in the right-hand panel at any time. After grouping by userid in A3, multiple subsets are obtained. Select A3, its result data will appear on the right-hand side:

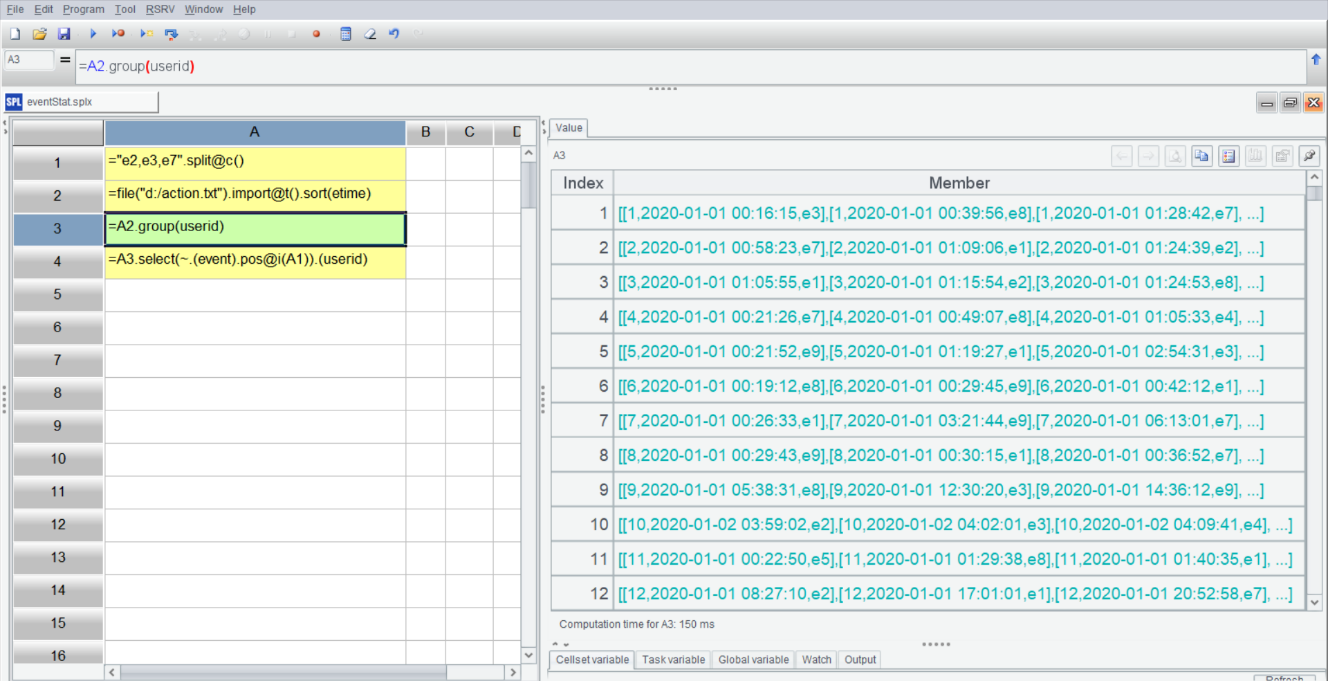
The group() function is simply for grouping and does not involve any aggregation operations. If you expand the members of the grouped result, you’ll see that it’s still a set, that is, a set consisting of each user’s events. The grouping operation does not disrupt the original order, and the grouped subsets will still be ordered by etime.

A4: Find the position where the A1 increasing sequence appears in each user’s event sequence, and finally use the select function to select users whose sequential event positions are not empty.

Once you are familiar with SPL, these steps can be simply written in one statement:

	A
1	=file("actions.txt").import@t().sort(etime)
2	=A1.group(userid) .select(~.(event).pos@i(["e2","e3","e7"])).(userid)

2. Retrieve users who have consecutively triggered events e2, e3, e7

To find consecutive events, when processing each e2 event for a single user in a loop, simply check if the next event is e3, and if the event after e3 is e7.

SQL code:

with t as (
    select userid,etime,event,
        row_number() over(partition by userid order by etime) rn 
    from actions)

select distinct t1.userid
from t t1 join t t2 join t t3 
    on t1.userid=t2.userid and t2.userid=t3.userid and t1.rn+1=t2.rn and t2.rn+1=t3.rn
where t1.event='e2' and t2.event='e3' and t3.event='e7';

Due to the unordered nature of SQL sets, it is impossible to retrieve data directly by position. To address this, you need to use window functions to manually generate a sequence number first, and then utilize the sequence number in the join conditions to calculate and express sequential relationships, which is also somewhat roundabout.

SPL sets, in contrast, are ordered, and it can also retrieve data by position. This allows for directly coding that follows a natural approach.

	A
1	=file("actions.txt").import@t().sort(etime)
2	=A1.group(userid)
3	=A2.select(~.(event).pselect(~=="e2" && ~[1]=="e3" && ~[2]=="e7")).(userid)

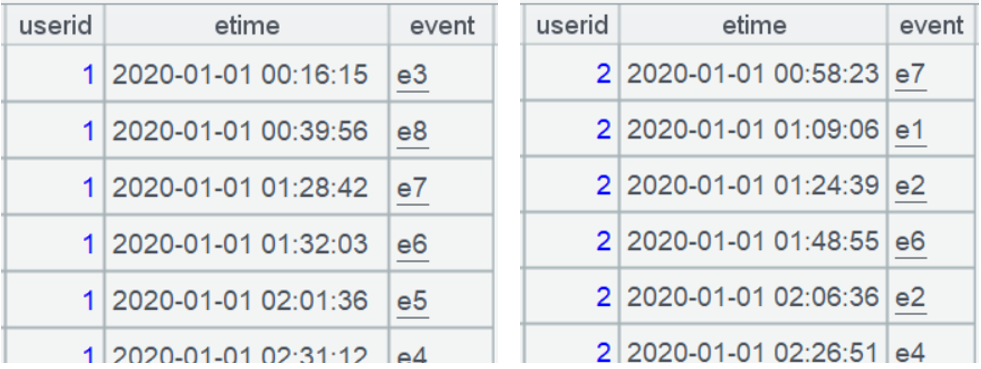
A3: For each grouped subset (denoted by ~, representing the current user’s records), use ~.(event) to extract the values of the event field to form a sequence. For instance, here’s User 1’s event sequence:

For each member of this sequence, use pselect to determine if the current member ~ and the two immediately following members ~[1] and ~[2] match the target event. If a match is found, pselect will return the position of that member; if no member matches, it will return null. The outermost select function will select all non-null groups, which are the user groups that have consecutively triggered events e2, e3, and e7. Finally, use .(userid) to obtain a result sequence consisting of the user IDs.

For this problem, SPL’s pos function can directly find consecutive subsequences (indicated by @c option), and A3 can be written in a simpler way:

3	=A2.select(~.(event).pos@c(["e2","e3","e7"])).(userid)

3. Find users and their event lists who have sequentially triggered any three events from the given multiple events

From a given set of multiple events, calculate all sequential event subsequences of length 3. For instance, given events e2, e3, e7 and e6, the resulting subsequences would be [e2, e3, e7], [e2, e3, e6], [e2, e7, e6], and [e3, e7, e6]. Now we want to find users who have triggered these event sequences.

Due to the inability of single SQL statement to execute procedural computations, it is difficult to compute these sequential events. You would have to assume that these event sequences are known in advance. Use the method from the previous problem to find users who have triggered each of these event sequences, and then get the union of those user sets.

SPL easily handles procedural computations step-by-step, and even supports recursion. With its ordered sets and the ability to reference by position, SPL can handle any number of given events and any target event sequence length.

	A	B	C
1	="e2,e3,e7,e6".split@c()
2	=file("actions.txt").import@t().sort(etime)
3	=A4.group(userid)
4	=A3.select(incseq(~.(A1.pos(event)).select(~),3))
5	func incseq(s, n)
6		if n>s.len()	return false
7		if n==1	return true
8		return s.cor( incseq(~[1:].select(~>s.~), n-1) )

If we assign numbers 1, 2, 3 and 4 to the given events e2, e3, e7 and e6 respectively, and convert user’s event sequence into a number sequence, then searching for a length-3 sequential event subsequence is equivalent to searching for increasing subsequences of length at least 3 within the converted number sequence.

Lines 5 through 8 define the incseq function, which is used to determine if any number sequence contains an increasing subsequence of a specified length.

Assuming user1’s event number sequence is [2,3,1,4,1,3], which contains the increasing subsequence 2,3,4, then incseq([2,3,1,4,1,3], 3) would return true.

Assuming user2’s event number sequence is [4,2,3,1,1,3], which doesn’t contain an increasing subsequence of length 3, then incseq([4, 2, 3, 1, 1, 3], 3) would return false. However, it contains an increasing subsequence of length 2, so incseq([4,2,3,1,1,3], 2) would return true.

A4: Employ the pos function to convert each user’s event sequence from A3 to the previously mentioned number sequence. For event not within the given event set, pos will return null, which will then be filtered out by the subsequent select function. Then, use incseq to check if each user has an increasing subsequence of length 3 (which is equivalent to a length-3 sequential event sequence).

The main logic of the incseq function is in B8, where ~[1:] represents the subsequence of members after the current member; select(~>s.~) is to filter out members within this subsequence that are greater than the current member. Here, s.~ is the current member of the outer loop function s.cor(), and the current member of the inner .select() is represented directly by ~. Then, recursively check if the sequence formed by the filtered members contains an increasing subsequence of length n-1. If it does, then, when combined with the current member, it forms an increasing subsequence of length 1, and the function incseq can return true. Here, the logical OR function cor is used. It immediately terminates the loop and returns when a true value is found, without continuing further calculations.

4. Query all consecutive event sequence information with a length greater than 3 for each user

‘Consecutive events’ refers to events with consecutive sequence numbers. The shortest consecutive event sequence contains two events, such as [e1, e2], [e2, e3], [e3, e4]. The longest consecutive event sequence is [e1, e2, …, e9].

There are 21 consecutive event sequences whose length exceeds 3 (6+5+…+1=21). Should we calculate every consecutive event sequence one by one and then perform the union, as in the previous problem, the resulting SQL code would be very long.

In addition, this task is not just about finding users; it also needs to retrieve detailed information about consecutive event sequence (start time, end time, consecutive event string).

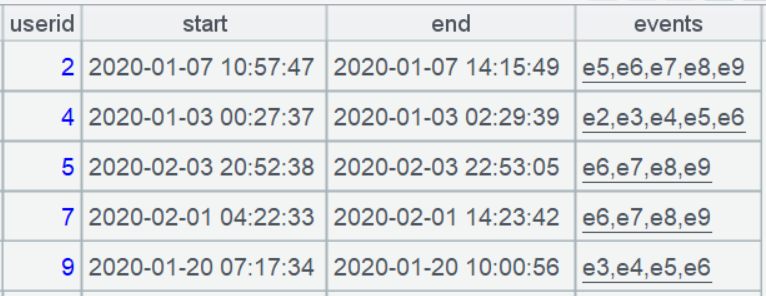
Since SQL doesn’t have the concept of grouped subsets, it’s unable to calculate such information for each small set of consecutive events. Trying to work around this with an alternative approach is difficult, so we won’t try here.

In contrast, SPL, by leveraging its features, such as ordered sets, calculation on grouped subsets, and positional access, makes it easy to gradually achieve this type of complex calculation in a natural way.

	A
1	=file("actions.txt").import@t().sort(etime)
2	=A1.group(userid)
3	=A2.(~.group@o(int(right(event,1))-#).select(~.len()>3))
4	=A3.conj()
5	=A4.new(userid, ~(1).etime:start,~.m(-1).etime:end,~.(event).concat@c():events)

A2: Group by user to obtain the event subset for each user:

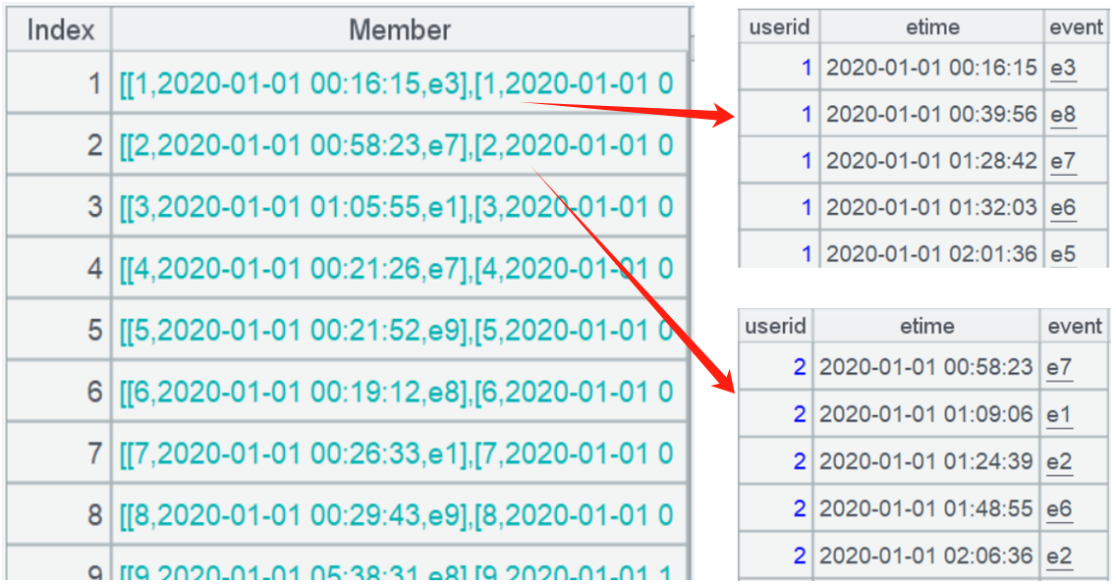
A3: Perform an ordered grouping on each user’s event subset. Specifically, use the group function to group the already ordered set, where @o indicates that only adjacent values are compared. The grouping expression calculates the difference between the event’s own sequence number (the number after ‘e’, ranging from 1 to 9) and its relative position within the subset (denoted by #). If the events are consecutive, both sequence numbers increment by 1 each time, so subtracting them will result in equality, causing them to be grouped together. This way, all subsets of consecutive events can be found. After that, filter to keep subsets with over 3 members, meaning at least 3 consecutive events have occurred.

The results are as follows: users 39, 42, and 44 etc., did not have any consecutive event sequences longer than 3. User 40 had two such sequences, and users 41 and 43 each had one. Having identified the desired continuous events, all of the original information has been retained after operations such as continuous grouping.

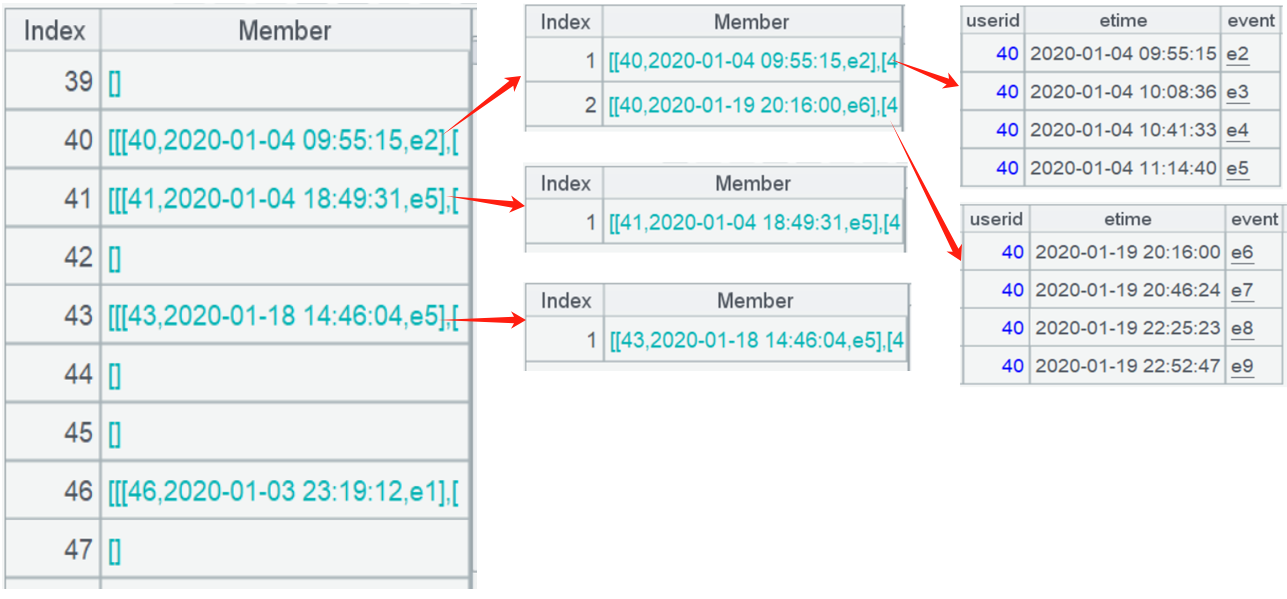This forms a three-level set, meaning that the values of A3 are set of sets of sets.

A4: Employ the conj function to merge the continuous event subsets of each user into a two-level set. You can observe that there are 4 consecutive event sequences for users 40, 41, and 43.

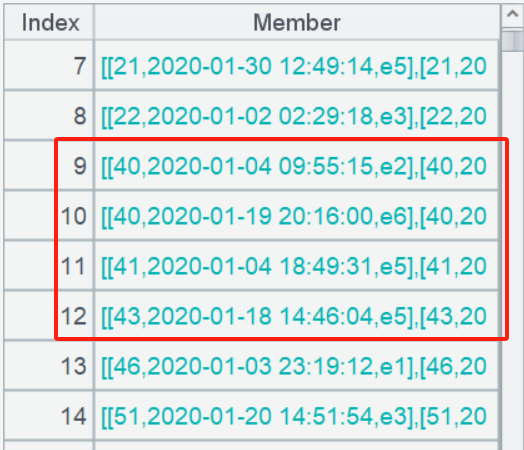
A5: Use the new function to calculate the start and end times, as well as the consecutive event substring, for each continuous event subset.

Once you are familiar with this, you’ll typically move the conj operation to an earlier position to simplify the code.

3	=A2.conj(~.group@o(int(right(event,1))-#).select(~.len()>3))
4	=A3.new(userid, ~(1).etime:start,~.m(-1).etime:end,~.(event).concat@c():events)

Download test data