The screening method is an ancient way of finding all prime numbers that do not exceed the natural number N (N>1). Arrange natural numbers 1 to N. The smallest prime number is 2, so first cross out 1. Starting from 2, leave 2, and cross out all numbers after 2 that can be divided by 2. Then the first number after 2 that is not crossed out is 3, leave 3 behind, and then cross out all numbers after 3 that can be divided by 3. The first number after 3 that is not crossed out is 5. Leave 5 and then cross out all numbers after 5 that can be divided by 5. Keep doing this, after each screening, the next adjacent number must be a prime number, so in the end, all composite numbers not exceeding N will be screened out, leaving only all prime numbers not exceeding N.

Create a sequence from 1 to 10000, cross out 1, start the loop with the smallest prime number 2, assign a multiple of the current number in the sequence to 0, and keep the current number itself. In this way, the next non-zero number will not be a multiple of all numbers smaller than it, and it will be the next prime number. The numbers in the final sequence that are not equal to 0 are all prime numbers within 10000.

http://try.scudata.com.cn/try.jsp?splx=ExA001sxfqzsb.splx

A2 generates a sequence of 1-10000 and assigns the first member a value of 0 in B2.

A3 loops each member of A2, B3 checks whether the current member is greater than 0. If it is, it indicates that it is the prime number that needs to be processed. C3 uses the step function to find the sequence of positions for all its multiples and uses to (2,) to extract the positions starting from the second one. C4 assigns a value of 0 to all members at these positions in the A2 sequence.

SPL can process sets with simple statements, such as to(A1) in A2 and A1.step(A3,A3) in C3, both of which will return sets. C4 can also perform batch assignment on sets.

After the loop is completed, A5 retrieves the members of the sequence that are greater than 0, which is the prime number list:

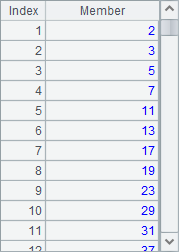
After becoming proficient, we can also write it directly using loop functions:

http://try.scudata.com.cn/try.jsp?splx=ExA001sxfqzsb2.splx

A2 uses the modify function to change the first member of the sequence to 0, which has the same effect as the second row in the previous method.

A3 uses a loop function to calculate in A2. For non-zero prime members, set the subsequent multiples to 0.

Loop functions can implement loop computation with a single function, without the need for code blocks in the for loop, resulting in more concise code. And SPL functions can be nested, with the step function as a parameter, and batch assignment can be done after finding the positions.