The cycle section refers to the numerical part that loops in an infinite cyclic decimal. Infinite cyclic decimals can be represented as fractions, so given the numerator and denominator of a fraction, its cycle section can be calculated.

Calculate the remainder using the numerator and denominator, and check if the remainder has appeared in the previous calculation. If the remainder has not appeared, it means that the cycle section has not appeared. Then multiply the remainder by 10 as the dividend and continue the loop calculation to find the remainder. If the remainder has occurred before, the loop ends. The quotient between the last occurrence of the same remainder and the current occurrence of the same remainder is the cycle section in an infinite cyclic decimal.

http://try.scudata.com.cn/try.jsp?splx=ExA003xhj.splx

A1 and B1 set the numerator and denominator of the fraction. C1 calculates the initial remainder using congruence.

A2 executes a loop until the remainder obtained in C1 is duplicated. B2 stores the remainders that have occurred during the loop process, which is also the basis for judging the execution of A2 loop. C2 calculates the next dividend, B3 stores the quotient that has occurred during the loop process, and calculates the quotient of the next digit. C3 updates the remainder in C1 to be new and continues the next loop.

In SPL, you can directly use cell names as parameter names and cell values as parameter values. This Excel like mode is very convenient for storing and analyzing data in code. In SPL, a conditional loop can be executed using for x. In the loop body, @ is used to represent the current cell value, such as B2=B2 | C1.

In this question, at the end of the loop, the historical remainders recorded by B2 and the historical quotients recorded by B3 are as follows:

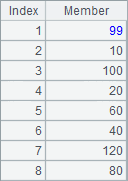
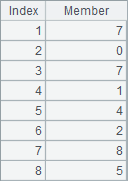
A7 extracts the corresponding part from the historical quotients and concatenates them with concat to obtain the cycle section. The result is as follows: