" The Sudoku game involves a grid of 81 squares. The grid is divided into nine blocks, each cont .."

pjf RaqForum 22 No.
1 Reply • 544 View • 4 Years ago

Puzzles & Games with esProc: Sudoku

The Sudoku game involves a grid of 81 squares. The grid is divided into nine blocks, each containing nine squares. The rules of the game are simple: each of the nine blocks has to contain all the numbers 1-9 within its squares. Each number can only appear once in a row, column or box. The following shows the existing numbers:

		7						8
8	4					6
			8	9	5	3
	1		4					3
							7
9			5				2	4
2		4			6
	8		7	3			1
1	3		9		4	7

Let’s look at how can we solve the Sudoku puzzle with esProc.

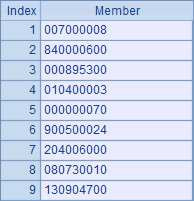
First we write the numbers in each row into a text file (sudoku01.txt) in the following format, where the blank squares are represented by zeros:

007000008

840000600

000895300

010400003

000000070

900500024

204006000

080730010

130904700

SPL script:

	A	B	C	D
1	=file("sudoku01.txt")	=A1.import@si()	=B1.(~.split@p())	=C1.conj()
2	[]	>func(A3,D1,1)	=A2(1)	=create(A,B,C,D,E,F,G,H,I).record(C2)
3	func		=ceil(B3/9)	=(B3-1)%9+1
4		if A3(B3)!=0	if B3==81	>A2=A2\|[A3.to()]
5			else	>func(A3,A3,B3+1)
6			return
7		=A3.to(C39-8,C39)	=A3.step(9,D3)
8		=ceil(C3/3)*3	=ceil(D3/3)*3	=(k=B8*9+C8-9,A3.m(k-20:k-18,k-11:k-9,k-2:k))
9		=to(9)\B7\C7\D8
10		for B9	>A3(B3)=B10
11			if B3==81	>A2=A2\|[A3.to()]
12			else	>func(A3,A3,B3+1)
13		>A3(B3)=0

B1 reads in the text file row by row and return it as a sequence:

undefined

C1 splits each of B1’s members, that is, numbers in the squares in each row, into a sequence:

undefined

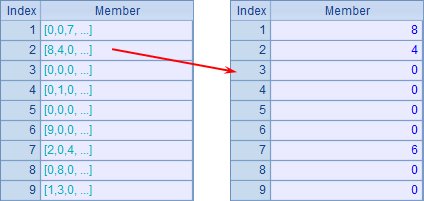
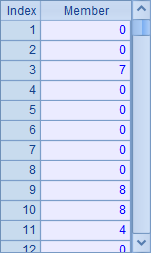
D1 concatenate numbers in all squares into a sequence:

undefined

A3 holds a subroutine. When executed, it accepts D1’s sequence as the parameter and passes the sequence number of the current square to B3. C3 and D3 respectively get the row and column on which the current square sits.

Line 4~line 6: Check if the current square contains a number, and call A3’s subroutine iteratively to find a number for the next square. When all squares are checked, write the numbers to A2’s sequence.

Line 7 ~ line 13: Enter a number for each blank square, which is represented by zero. A7 lists a sequence of numbers on same row, B7 lists a sequence of number on same column, and D8 lists a sequence of numbers in the current block. Since the current square’s number must be different from all the other numbers on the same row, column and box, B9 calculates difference of sequences to get all possible eligible numbers for the current square.

Line 10 ~ line 12: Try every possible number for the current square and call A3’s subroutine to find a number for the next square. When all squares are filled, write the numbers to A2.

If all numbers in B9 are tried but none is eligible, reset the number in the current square as 0 and modify the number in the previous square.

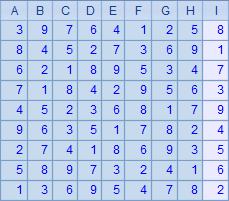
B2’s main program calls A3’s subroutine to fill squares with numbers from the first. Below is A2’s final result:

undefined

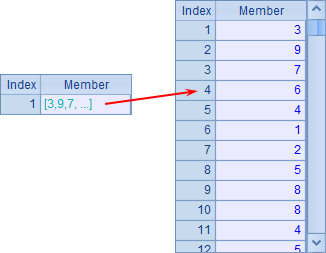
Generally A2 gets one result set. In certain cases a Sudoku puzzle has no solution or multiple solutions. For the convenience of viewing D2 populates the first set of numbers to a table sequence to get the final solution:

undefined