Download the PDF version for better reading experience

JOINs are long-standing SQL headaches. As the number of tables to be joined increases, coding becomes error prone. The complicated statements for achieving JOINs make associative queries always be a BI software weakness of. Almost no BI software can provide smooth multi-table associative queries. It is also hard for SQL to optimize and increase performance when the number of tables involved is relatively many or they contain a large volume of data.

Our JOIN operations series will take a deep dive to examine the SQL pain and propose a way to simplify the JOIN syntax and enhance performance.

Ⅰ JOINs in SQL

First let’s look at how SQL defines the JOIN operation.

The SQL JOIN definition is simple. In SQL, a JOIN is the Cartesian product between two sets (tables) filtered by a specific condition. The syntax is A JOIN B ON …. In principle, the result set of performing a Cartesian product should be composed of 2-tuples whose members come from both sets. As a SQL set is a table whose members are always the records made up of fields, and as SQL does not support using a generic data type to describe a 2-tuple whose members are records, the language simply joins fields of records from both tables to form a new set of records to return.  Rather than the multiplication (Cartesian product), that is the original meaning of the name JOIN, which joins fields of two records. But whether a result set consists of 2-tuples or records generated by combining fields from both tables will not affect our analysis.

The SQL JOIN definition does not stipulate the filtering condition form. Theoretically an operation whose result set is the subset of the Cartesian product of the two original sets is considered a JOIN. Suppose there are set A={1,2} and set B={1,2,3}, the result set of calculating A JOIN B ON A<B is {(1,2),(1,3),(2,3)}; and the result set of calculating A JOIN B ON A=B is {(1,1),(2,2)}. We call a join where the filtering condition contains one or more equations the equi-join, and one where the filtering condition is not an equation the non-equi-join. According to the definitions, the first join in the above is a non-equi-join and the second join is an equi-join.

An equi-join between two data tables may have a filtering condition that contains multiple equations concatenated by AND. The syntax is A JOIN B ON A.ai=B.bi AND …, where ai and bi are respectively fields of table A and table B. According to experience, most of the JOINs in real-world business situations are equi-joins. The non-equi-joins are rare. And on many occasions, a non-equi-join can be handled by being converted into an equi-join, so our analysis focuses on equi-joins and uses tables and records instead of sets and members in the following examples.

According to the different rules of handling null values, there are three types of equi-joins, INNER JOIN, which is the strictest equi-join, LEFT JOIN, and FULL JOIN (RIGHT JOIN can be understood as the reversed form of LEFT JOIN and thus will not be taken as a separate type). Based on the numbers of corresponding records (which are the 2-tuples satisfying a specific filtering condition) in two table respectively, there are also four types of joining relationships – one-to-one relationship, one-to-many relationship, many-to-one relationship, and many-to-many relationship. As these terms are always covered by SQL and database documentations, we will skip them here.

Let’s move on to take a look at JOIN implementations.

A simple way that is easy to think of is to perform hardcoded traversal without distinguishing the equi-join from the non-equi-join. Suppose table A has n records and table B has m records, the complexity of hardcoded traversal for computing A JOIN B ON A.a=B.b is nm, that is, a total number of nm filtering condition computations are needed.

It is a slow algorithm, apparently. Yet that is what some reporting tools that support multiple or diverse data sources use to achieve a join. In those reporting tools, the joining relationship (that is, the filtering condition in a JOIN) between data sets is split and scattered into the cell formulas and becomes invisible. Only traversal can be used to compute the joining expressions.

A fully developed database does not choose to be slow. Generally, HASH JOIN algorithm is used to achieve an equi-join. The algorithm divides the records of both associative tables into groups according to their joining keys’ HASH values (the joining keys are fields on both sides of the filtering condition equation, which are A.a and B.b). Each group contains records where the key fields have same HASH values. Suppose the HASH value range is 1…k, it will split table A and table B respectively into k subsets, which are A_1,…,Ak_ and B_1,…,Bk_. The HASH value of the joining key a in records of Ai is i and The HASH value of the joining key b in records of Bi is also i. We just need to traverse Ai and Bi to join up records. Since each HASH value corresponds to a different field value, it is impossible to correspond a record of Ai to one of Bj if i!=j. Suppose the number of records in Ai is ni and that in Bi is mi, a total number of SUM(ni*mi) is needed to compute the filtering condition. In an ideal case when ni=n/k and mi=m/k, the overall degree of complexity will be reduced to 1/k of that of the original hardcoded traversal. This is far more efficient.

So, to speed up a join between multiple data sources in a reporting tool, it would be the best to do the join at the data preparation phrase, otherwise performance will be reduced sharply if the involved data is relatively large.

The HASH function cannot ensure an even split each time. Sometimes a rather large group appears and there is just small effect for performance optimization. And it would be better to use a relatively simple HASH function, otherwise it will take longer to calculate HASH values.

When the data involved cannot fit into the memory, the database will adopt HASH HEAP method, which is the extension of HASH JOIN algorithm. The HASH HEAP method traverses table A and table B to divide records into multiple subsets according to their joining keys’ HASH values and buffer them to an external storage, which are called heaps. Then we can perform an in-memory JOIN operation on corresponding heaps. The join will occur between corresponding heaps because different HASH values correspond to different key values. The method thus transforms a JOIN between large data sets into one between pairs of smaller data sets.

It is probable that the HASH function generates a particularly large heap that cannot be wholly loaded into the memory. In that case a second HASH HEAP is needed, and a new HASH function is used to HASH heap the particularly large heap using the HASH HEAP method. In view of this, multiple buffers may happen during the execution of a JOIN operation on the external storage and the computing performance is not so manageable.

Similar process for performing a JOIN in a distributed system. The system transmits records among nodes according to joining keys’ HASH values, which is called Shuffle action, and then performs JOIN on single nodes. When there are a lot of nodes, the network transmission delay will compromise a part of the performance increase obtained through multi-nodes execution, so a distributed database system generally sets a limit for the number of nodes. When the limit is exceeded, more nodes will not bring better performance.

Ⅱ Equi-joins

Let’s look at three types of equi-joins:

1. Foreign-key join

Two tables are associated by matching a certain field in table A with the primary key of table B (By field association, as we explained in the previous essay, it is the equivalence of corresponding values in fields specified by the joining condition). Table A is called the fact table, and table B the dimension table. The field in table A that will match table B’s primary key is table A’s foreign key that points to table B; table B is thus table A’s foreign key table.

In this context, the primary key is a logical one, including one or more fields whose values are unique and that identify records uniquely. The primary key is not necessarily the one set on the database table.

The relationship between a table and its foreign key table is many-to-one, which supports JOIN and LEFT JOIN only. The FULL JOIN is extremely rare.

A typical example is the relationship between Production transaction table and Product information table.

The foreign-key-based association is asymmetrical. And positions of fact table and dimension table cannot be swapped.

2. Homo-dimension join

Two tables are associated by matching table A’s primary key and table B’s primary key. The matching is a one-to-one relationship, and each table is the other’s homo-dimension table. The join between homo-dimension tables supports JOIN, LEFT JOIN and FULL JOIN. But for most of the data structure designs, FULL JOIN is rare.

A typical example is the relationship between Employees table and Managers table.

The relationship between two homo-dimension tables is symmetrical and their positions are equal. Homo-dimension tables can also form an equivalence relationship. Suppose A and B are homo-dimension tables, B and C are homo-dimension tables, then A and C are also homo-dimension tables.

3. Primary-sub join

Two tables are associated by matching table A’s primary key and one or several of table B’s primary key fields. Table A is the primary table, and table B is the sub table. It is a one-to-many relationship from table A to table B. The join between them only involves JOIN and LEFT JOIN.

A typical example is the relationship between Orders table and Order details table.

The relationship between the primary table and the sub table is asymmetrical and the matching has a fixed direction.

SQL does not differentiate the concept of foreign key join and the primary-sub join. In the context of SQL, the many-to-one relationship and the one-to-many relationship are essentially the same thing except for the direction in which tables are associated. Indeed, an orders table can be considered the foreign key table of the order details table. The purpose of distinguishing them is to use different methods to simplify their syntax and optimize their performance.

The three types of joins cover most of the equi-join scenarios. Almost all equi-joins that have business significance fall into the three types. To divide equi-joins into the three types will not decrease the range of its application scenarios.

All the three types of equi-joins involve the primary key. There is no many-to-many relationship. But, is it unnecessary to take the relationship into account on all occasions?

Yes. The relationship almost does not have any meaning in real-world business practice.

A many-to-many correspondence occurs when the associative fields for JOINing two tables do not contain the primary key. In that case on almost all occasions, there exists a larger table that correlates the two tables with each other by using them as dimension tables. When the Student table and the Subject table are JOINed, there will be a Score table that uses them as dimension tables. It makes no sense in real-world business practice to purely JOIN such two tables.

So, it is almost certain that a SQL statement is wrong or that the data is bad if a many-to-many relationship occurs. The relationship is useful for checking mistakes in JOIN operations.

But we do not deny the existence of an exception by using “almost”. On rare occasions, the many-to-many relationship has business significance. One example is performing matrix multiplication in SQL, where an equi-join with many-to-many relationship occurs. Try to code the query by yourselves.

It is indeed a simple way to define JOIN operations as the filtered Cartesian product. The simple definition covers a more variety of joins, including the equi-joins with many-to-many relationship as well as the non-equi-joins. On the other hand, it is too simple to fully reflect the computing characteristics of the most common equi-joins, depriving SQL of opportunities to better code a query for achieving a computing goal according to the characteristics and bringing great difficulty in expressing and optimizing a complex query (a join involving several or more tables or with a nested query). But by making good use of the characteristics, we can design simple syntax to make computations more performant. We will discuss it in detail in subsequent essays.

In a word, it is more sensible to define the rare JOIN scenarios as a special type of operations than to include them in a universal definition.

Ⅲ Simplifying JOIN syntax

As all joins involve the primary key, we can devise ways of simplifying JOIN code according to this characteristic. There are three join simplification methods.

1. Foreign key attributization

Below are two tables:

employee table made up of the following fields:

• id

• name

• nationality

• department

department table made up of the following fields:

• id

• name

• manager

Both tables use id field as the primary keys. The department field of employee table is a foreign key pointing to the department table. The manager field of the department table is a foreign key pointing to the employee table (because managers are also employees). This is the conventional table structures.

Now we want to find the US employees whose managers are Chinese.

SQL does this by JOINing three tables:

SELECT A.*
FROM employee A
JOIN department B ON A.department=B.id
JOIN employee C ON B.manager=C.id
WHERE A.nationality='USA' AND C.nationality='CHN'

First, FROM employee is used to obtain employee information; JOIN employee table and department table to get employees’ department information; JOIN department table and employee table to get information of managers. The employee table is involved into two JOINs and aliases are needed to distinguish the table in two JOINs, making the whole statement bloated and difficult to understand.

We can write the statement in the following way if we regard the foreign key field as the corresponding records in the dimension table:

SELECT *
FROM employee
WHERE nationality='USA' AND department.manager.nationality='CHN'

But this isn’t a standard SQL statement.

The code highlighted in bold in the second statement means “nationality of manager of department of the employee in the current record”. Since we regard the foreign key field as corresponding records in the dimension table, the foreign key table fields can be regarded as attributes of the foreign key field. Thus department.manager is “the manager of the department of the current employee”. Since the manager field is the foreign key in the department table, fields of records in the dimension table to which it points can be still treated as its attributes, which generates the code department.manager.nationality – “the nationality of the manager of the department of the employee”.

Obviously, the object-oriented thinking, which is called foreign key attributization, is more natural and intuitive than that based on filtered Cartesian product. Foreign-key-based joins do not involve multiplication between two tables. The foreign key field is only used to find corresponding records in the foreign key table, without being involved in the Cartesian product operation having multiplication property.

As previously stipulated, the associative field in the dimension table for a foreign-key join must be the primary key. So, one foreign key value matches one record in the dimension table. This means that each department value in the employee table relates to only one record in the department table, and that each manager field value in the department table associates with only one record in the employee table. That ensures that, for each record in the employee table, department.manager.nationality is unique and can be uniquely defined.

As the SQL JOIN definition does not involve the primary key, we cannot make sure that each foreign key value of the fact table corresponds to only one record in the dimension table. It may relate to multiple records, and for each record of employee table, department.manager.nationality cannot be uniquely defined and thus becomes invalid.

The object-oriented syntax is common in high-level languages (like C language and Java), which stores data in objects. Though department field values in the employee table are displayed as numbers, they essentially represent objects. In many data tables, the primary key values do not have substantial meanings, but are only used to identify records. Similarly, the foreign key field is just for locating the matching records in its foreign key table. If the foreign key values are directly stored as objects, numbers will become unnecessary. But as SQL does not support the object storage, numbers are still needed.

In a foreign-key-based relationship, the fact table and the dimension table are not in an equal position. We can look up a field in a dimension table according to the fact table, but not vice versa.

2. Interconnection of homo-dimension tables

The join between homo-dimension tables is simpler. Considering the following two tables:

employee table

• id

• name

• salary

• …

manager table

• id

• allowance

• ….

Both tables use id field as their primary keys. Managers are also employees, so the two tables share the ids. Since managers have more attributes, their information is stored in a separate table.

Now we want to find the total income (including the allowance) of each employee (including every manager).

A JOIN operation is necessary for SQL to do it:

SELECT employee.id, employee.name, employy.salary+manager.allowance
FROM employyee
LEFT JOIN manager ON employee.id=manager.id

But for two tables having a one-to-one relationship, we can treat them like one table:

SELECT id,name,salary+allowance
FROM employee

According to the stipulation, homo-dimension tables are JOINed according to the primary keys. Records with same primary key values correspond exclusively to each other. The expression salary+allowance is uniquely computed over each record of the employee table, having no possibility of causing ambiguity. We call this simplification method Interconnection of homo-dimension tables.

Homo-dimension tables are equal. Each one can refer a field of the other.

3. Sub table set-lization

A typical example of the primary and sub tables is the orders table and the order detail table, like the following two tables:

Orders table

• id

• customer

• date

• …

OrderDetail table

• id

• no

• product

• price

• …

The Orders table’s primary key is id field. The OrderDetail table’s primary key is made up of id and no fields. The former is a part of the latter.

We want to know the total amount of every order.

Below is the SQL:

SELECT Orders.id, Orders.customer, SUM(OrderDetail.price)
FROM Orders
JOIN OrderDetail ON Orders.id=OrderDetail.id
GROUP BY Orders.id, Orders.customer

SQL needs a GROUP BY to reduce the number of records with same ids produced by JOIN operation.

If we treat records of the sub table OrderDetail that match the primary table’ primary key as a field of the latter, the JOIN and GROUP BY won’t be necessary:

SELECT id, customer, OrderDetail.SUM(price)
FROM Orders

Unlike a familiar field, values of OrderDetail field are sets when certain records of the table are considered a field of the Orders table because the relationship between a primary table and its sub table is one-to-many. Here an aggregation is performed over each set type value to get a single value. This simplification method is called sub table set-lization.

This perspective on primary and sub table association makes the query easy to write and understand, as well as less error prone.

Suppose the Orders table has another sub table that records payment information:

OrderPayment table

• id

• date

• amount

• ….

We want to find the orders that have not yet been fully paid, or whose accumulated payments are less than the total amount.

We shouldn’t simply JOIN the three tables. A many-to-many relationship will occur between the OrderDetail table and the OrderPayment table and the result will be wrong (just think about the high probability of error occurrence by performing a many-to-many join mentioned in the previous essay). The right way is to GROUP the two tables separately and JOIN the grouped results with Orders Table. The query will include a subquery:

SELECT Orders.id, Orders.customer,A.x,B.y
FROM Orders
LEFT JOIN ( SELECT id,SUM(price) x FROM OrderDetail GROUP BY id) A
    ON Orders.id=A.id
LEFT JOIN ( SELECT id,SUM(amount) y FROM OrderPayment GROUP BY id ) B
    ON Orders.id=B.id
WHERE A.x>B.y

If we treat each sub table as a field of the primary table, the query will be simple and easy:

SELECT id,customer,OrderDetail.SUM(price) x,OrderPayment.SUM(amount) y
FROM Orders
WHERE x>y

This way, a many-to-many relationship error can be avoided.

The primary table and its sub table are not equal. But a two-way reference is useful. In the above we talked about the case of referencing records of the sub table in the primary table. The reference in an opposite direction is similar to that from a foreign key table.

By treating a multi-table association operation as a relatively complex single table operation, we abandon the Cartesian product to look at JOIN operations from a different perspective. The new approach eliminates associative actions from the most common equi-join operations and even the JOIN key word from the syntax, creating simple and easy to understand queries.

Ⅳ Dimension alignment

In the previous essay, we talked about the alignment of two sub tables to the primary table. Below is the SQL query for doing it:

SELECT Orders.id, Orders.customer, A.x, B.y
FROM Orders
LEFT JOIN (SELECT id,SUM(price) x FROM OrderDetail GROUP BY id ) A
    ON Orders.id=A.id
LEFT JOIN (SELECT id,SUM(amount) y FROM OrderPayment GROUP BY id ) B 
    ON Orders.id=B.id
WHERE A.x > B.y

Obviously, this is a useful JOIN in real-world queries, but under which type it should be classified?

It involves the Orders table and two subqueries – A and B. Each subquery has a GROUP BY id clause which means the result set’s primary key will be the id field. Now the three tables (a subquery can be considered a temporary table) involved in the JOIN use the same primary key. They are homo-dimension tables associated by a one-to-one mapping. That fits into our types.

But the syntax used to simplify JOIN queries in the previous relative essay cannot be applied to this homo-dimension table JOIN query because both subqueries cannot be omitted.

The prerequisite for a simplifiable JOIN query should be that the relationship between the to-be-joined tables is already defined in the whole data structure. In technical terms, we need to know the database metadata definition. It is unlikely that an ad hoc subquery can be predefined in the metadata, so the table to be joined (a subquery) should be specified.

While the temporary tables to be JOINed cannot be omitted, but since the associative fields, which are primary keys, are already specified in GROUP BY and the grouping fields, which are also primary keys defined by GROUP BY in the subqueries, must be selected for performing the outer JOINs, and moreover, the sub tables over which the subqueries are performed are independent of one another without associations any more, we can put both the GROUP and aggregate operations in the main query to get rid of a layer of subquery:

SELECT Orders.id, Orders.customer, OrderDetail.SUM(price) x, OrderParyment.SUM(amount) y
FROM Orders
LEFT JOIN OrderDetail GROUP BY id
LEFT JOIN OrderPayment GROUP BY id
WHERE A.x > B.y

The join we are discussing is far from the JOINs defined in SQL. There is no trace of Cartesian product in it. And unlike a SQL JOIN defined between any two tables, this join aligns tables – OrderDetail, OrderPayment and Orders – to a common primary key field, the id field. All tables are aligned against a certain base dimension. As they have different dimensions (primary keys), the GROUP BY action may be needed during the process, leading to an aggregate operation when referring to a field of the table being grouped. There are no direct associations between the OrderDetail table, the OrderPayment table, and even the Orders table, so there is no need to care about their relationships, or whether there is another table to be joined with the current table. In SQL, the Cartesian product-based JOIN requires at least two tables to define the associative operation. Any change to an involved table or its deletion requires the handling of the matching table, making the query hard to understand.

Ours is the dimension alignment join. Though still within the three types previously defined, it has a different syntax. Unlike the case in SQL, here the JOIN key word is more a conjunction than a verb. The FULL JOIN isn’t a rare thing for the dimension alignment, whereas it is impossible or scarcely seen with the three basic join types.

Though an example of the primary and sub tables is used to explain the dimension alignment join, it isn’t the exclusive scenario to which this kind of join is applied (According to the simplified syntax for a join between the primary and sub tables, the query should not be so complicated). The dimension alignment join syntax can be applied to any tables to be associated, without the requirement that the associative fields be primary keys or a part of them.

Here are the Contract table, the Payment table, and the Invoice table:

Contract table

• id

• date

• customer

• price

• …

Payment table

• seq

• date

• source

• amount

• …

Invoice table

• code

• date

• customer

• amount

• …

To find each day’s contract amount, payment amount, and invoice amount, we can write the query like this:

SELECT Contract.SUM(price), Payment.SUM(amount), Invoice.SUM(amount) ON date
FROM Contract GROUP BY date
FULL JOIN Payment GROUP BY date
FULL JOIN Invoice GROUP BY date

Here we specifically write a GROUP BY date clause to specify that the result set will be aligned by date, rather than put the clause within SELECT statement.

The arrangement focuses on each table separately without need to take care of the association relationships between the three tables. It gives the impression that there are no associations among the tables except for the dimension (date) to which they are pulled.

We can also use a mix of the join types:

Along with the above Contract table, here are the Customer table and the Sellers table:

Customer table

• id

• name

• area

• …

Sales table

• id

• name

• area

• …

The customer field in the Contract table is the foreign key pointing to the Customer table.

To find the number of salespeople and the contract amount in each area:

SELECT Sales.COUNT(1), Contract.SUM(price) ON area
FROM Sales GROUP BY area
FULL JOIN Contract GROUP BY customer.area

The query uses both the dimension alignment join syntax and the foreign key attributization syntax.

In these examples, all the joins are finally become the homo-dimension type. A dimension alignment join can also be of primary-sub-table type. But it is quite uncommon so we will skip it here.

Finally, the above dimension alignment join syntax, for the time being, is just schematic. It needs a clear and strict dimension definition to become fully formalized and generate interpretive execution statements.

We call the simplistic syntax DQL (Dimensional Query Languange). This is a query language revolving around dimensions. The language has been successfully implemented in engineering and released as RaqReport’s DQL server. The server serves to translate DQL statements to SQL ones, which means it can run on any relational databases.

Read related essays and articles in RaqForum if you want to know more about DQL theory and applications.

Ⅴ Final JOIN query solution

By rethinking and redefining the equi-joins, we are able to simplify the join syntax. A direct effect is that queries become easy to write and understand. We offer three solutions – foreign key attributization, of homo-dimension table interconnection, and sub table set-lization – to eliminate the explicit JOIN actions, making queries more conform to our natural thinking. The dimension alignment join syntax frees programmers from taking care of relationships between tables to let them create simple queries.

What’s more, the simplified join syntax helps avoid mistakes.

SQL allows writing join conditions in WHERE clause (which goes to the conventional Cartesian product-based join definition), and many programmers are accustomed to do so. There isn’t any issue when there are only two or three tables to be joined, but it is very likely that some join conditions are missed out if there are seven or eight or even a dozen of tables. The omission will cause a many-to-many complete cross join while the SQL statement is executing properly, leading to a wrong result (As previously mentioned, it is most probably that the SQL statement is wrong when a many-to-many join occurs) or a crashed database because of the quadratic scale of the Cartesian product if the table over which the join condition is missed out is too big.

We will not miss out any join condition by adopting the simplified join syntax because the syntax isn’t Cartesian product-based and denies the significance of the many-to-many relationship. With the syntax, the complete cross product is impossible.

SQL uses subqueries to handle a JOIN where sub tables need to be first grouped before aligning to the primary table. When there is only one sub table, we can JOIN tables first and then perform GROUP without using a subquery. Habitually and in an effort to avoid the subqueries, some programmers apply this rule to a JOIN with multiple sub tables by first writing JOIN and then GROUP, only to get a wrong result.

The dimension alignment join syntax will save programmers from this kind of mistake. It handles any number of sub tables in the same way without using subqueries.

The greatest impact of redefining JOIN operations is making associative queries convenient to achieve.

Now the agile BI products are popular. Vendors offer products claiming that they enable the businesspeople to perform queries and reports through drag and drop. The real-life effect, however, is far below expectation. IT resources are still a necessity. The reason behind this is that most of the business queries involve procedural computations that cannot be handled through drag and drop. Yet there are certain business queries that are non-procedural but still cannot be managed by businesspeople themselves.

Those are the status quo of join query service offered by most of the BI products. The service is a weakness of them. In our previous essays, we explained that it is the oversimplified SQL JOIN definition that is responsible for the difficulties in implementing join queries.

A BI product’s querying model is that IT professionals pre-construct the model and the businesspeople make queries based on the model. The modeling is in fact the construction of a logical or physical wide table. Different queries need different models, which we call on-demand modeling. In this case, a BI product has already lost its intended agility.

A different angle in looking at the JOIN operations will address the associative query issue at the root. The three join types we summed up and the corresponding solutions treat the multi-table associations as queries over one table, which, for the businesspeople, is easy to understand, though the attributes (fields) of a table become a little complicated. An attribute may have the sub-attributes (Referenced fields of the dimension table pointed by a foreign key), and a sub-attribute may also have the sub-attributes (with a multi-layer dimension table). Sometimes the field values are sets instead of single values (when a sub table is regarded as the field of the primary table). The perspective makes an ordinary join (A Chinese manager’s American employees are such an example), even a self-join, easy to understand, and a join where one table having same dimension fields not an issue any more (because each attribute has its own sub-attributes).

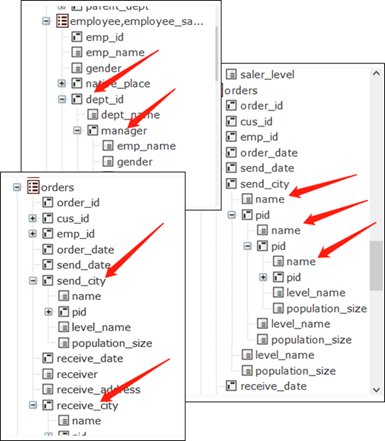
With this association mechanism, IT pros only need to define the data structure (metadata) once and create a certain interface (where table fields are listed in hierarchical tree structure instead of the commonly seen linear structure). The businesspeople can then perform joins independently without turning to the IT department. Modeling is needed only when a change to the data structure happens, rather than whenever a new associative query need appears. That constitutes the non-on-demand modeling. A BI product becomes agile only when it uses such a mechanism.

Ⅵ Foreign-key pre-join

Let’s move on to look at how to increase JOIN query performance by making use of certain features of JOINs. As this involves lots of details, we’ll just list some easy-to-understand cases. You can find the complete illustrations in Performance Optimization e-book and related articles in RaqForum.

Let’s begin from the in-memory foreign-key-based join operations:

Here are two tables:

customer table made up of fields below:

• key

• name

• city

• …

orders table made up of fields below:

• seq

• date

• custkey

• amount

• …

The custkey field in the orders table is the foreign key pointing to key field, the customer table’s primary key.

To find out the total orders amount in each city (to make the discussion simpler, we won’t specify any condition), we can express the query in SQL as follows:

SELECT customer.city, SUM(orders.amount)
FROM orders
JOIN customer ON orders.custkey=customer.key
GROUP BY customer.city

Generally, the database uses HASH JOIN algorithm to calculate HASH values of the associative keys respectively in the two tables and match the values. 

We can write the algorithm using the simplified JOIN syntax (DQL) introduced in previous section:

SELECT custkey.city, SUM(amount)
FROM orders
GROUP BY custkey.city

This implies that a better optimization plan is possible. Let’s look at how to do it.

Suppose all data can be loaded into the memory, we can optimize the query by switching foreign key values into addresses.

By switching values of the foreign key field, custkey, in the fact table orders to addresses of corresponding records in the dimension table customer – that is, converting the custkey values to records of the customer table – we can directly reference a field of the customer table for calculation.

As it’s inconvenient to describe the detailed computing process in SQL, we demonstrate it in SPL by using a file as the data source:

	A
1	=file("customer.btx").import@b()
2	>A1.keys@i(key)
3	=file("orders.btx").import@b()
4	>A3.switch(custkey,A1)
5	=A3.groups(custkey.city;sum(amount))

In the above SPL script, A1 reads data from customer table; A2 sets the primary key for customer table and creates index on the key.

A3 reads orders table; and A4 replaces values of A3’s foreign key field custkey with corresponding records in A1. After the script is executed, orders table’s custkey field will be converted into the corresponding record of customer table. A2 creates an index to facilitate the subsequent switch. Since the fact table is generally far larger than the dimension table, the index can be reused.

A5 performs grouping and aggregation. Since each custkey field value is now a record, we can directly reference a field using the operator during the traversal of orders table. custkey.city can be correctly executed now.

After the switch action defined in A4 is finished, the custkey filed of A3’s in-memory fact table already has values that are addresses of corresponding records in A1’s dimension table. The process is called foreign key address-alization. Now we can directly retrieve a field of the dimension table without looking it up in A1 by matching the foreign key value. It takes just some time of constant magnitude to get a field from the dimension table by avoiding HASH value calculation and matching.

Yet usually we still use the HASH method to create the primary key index in A2 by calculating the key’s HASH values, and to calculate custkey’s HASH values to match A2’s HASH index table at A4’s switch action. In terms of computational amount, the foreign key address-alization strategy and the conventional HASH partitioning method are almost neck and neck in handling one single JOIN.

If data can be wholly loaded into the memory, the advantage of foreign key address-alization strategy is that the addresses can be reused. This means that we just need to do the calculation and comparison of hash values once (A1-A4). Later the results are ready to be used by a join operation on the same two associated fields, significantly boosting performance.

The strategy can be devised because the foreign key has unique corresponding records in the dimension table – that is, one foreign key value matches only one record in the dimension table, so we can convert each custkey into its corresponding record in A1.With SQL JOIN definition, we cannot assume that each foreign key points to a unique record in the dimension table and thus the strategy is unimplementable. Moreover, SQL does not have record address data type and each join needs HASH value calculation and matching.

If there are multiple foreign keys in a fact table that refer to multiple dimension tables, the conventional HASH partitioning JOIN strategy can only handle one JOIN at a time. For a number of JOINs, each has to perform all the operations and needs to store its intermediate result for use in the next JOIN. The computing process is intricate, and data will be traversed many times. The foreign key address-alization strategy in that case, however, just traverses the fact table once without generating intermediate results, creating a clear computing process.

Memory is parallelism-friendly, but the HASH partitioning JOIN algorithm isn’t easily paralleled. Yes, we can segment tables to calculate hash values in parallel. But the strength of the parallel processing will be offset by the resource conflict that occurs when records with same hash values in two corresponding segments are being located and gathered for comparison. Under the foreign-key-based join model, two tables being joined are not equal by defining one as the fact table and the other as the dimension table, and we just need to segment the fact table to perform parallel processing.

By reforming it with the foreign key attributization concept, the HASH partitioning strategy’s ability of handling multi-foreign-key joins and performing parallel processing can be increased. Some database products can do this kind of engineering optimization. But when more than two tables are JOINed and when multiple JOIN types are involved, it isn’t easy for the database to judge which table should be identified as the fact table to be traversed and processed in parallel and which tables should be used as the dimension tables on which the HASH indexes are built, making the optimization effect unguaranteed. So sharp decline in performance often occurs when the number of tables being JOINed increases (performance significantly decreases when 4 or 5 tables are being JOINed but there isn’t significant increase in the size of the result set). By introducing the foreign key concept to the JOIN model for handling multi-foreign-key joins specifically, the foreign-key-based joins can define fact table and dimension tables clearly. The increase of the numbers of tables to be JOINed will only lead to a linear decline in performance.

At present in-memory database technologies are hot. But our analysis shows that it’s almost impossible for the SQL-based in-memory databases to handle JOIN operations fast.

Ⅶ More foreign-key joins

Let’s continue our discussion of foreign-key-based JOINs using the example in the previous article.

If a fact table is too big to be held by the memory, the foreign key address-alization strategy will fail because the external storage cannot store the pre-calculated addresses.

Generally, a dimension table referred by a foreign key is small while an ever-increasing fact table is much larger. By loading the smaller dimension table into the memory, we can create temporary foreign key pointers.

	A
1	=file("customer.btx").import@b()
2	>A1.keys@i(key)
3	=file("orders.btx").cursor@b()
4	>A3.switch(custkey,A1)
5	=A3.groups(custkey.city;sum(amount))

The first two steps are the same as those for an in-memory computation. In step 4, switch from values to addresses is performed while data is streaming in, but the switch result cannot be retained for reuse. Hash value calculations and comparisons are still needed for the next JOIN. The performance would thus be poorer than that of the in-memory strategy. Compared with the HASH JOIN algorithm in terms of the computational amount, this one does not need to calculate hash values of the dimension table’s primary key. The algorithm gains an advantage especially when the hash index on the dimension table is repeatedly used, but its ability in increasing the overall performance is limited because of the generally small size of a dimension table. Yet it is as capable of handling all foreign keys at a time and as easy to be paralleled as an in-memory algorithm, thus producing much better real-world performance than the HASH JOIN algorithm.

From this algorithm, we have its variation – foreign key numberization.

By converting of dimension table’s primary key values into natural numbers beginning from 1, we can identify records in a dimension table by their numbers without the need of calculating and comparing hash values, obtaining high performance the in-memory foreign key address-alization strategy can give.

	A
1	=file("customer.btx").import@b()
2	=file("orders.btx").cursor@b()
3	>A2.switch(custkey,A1:#)
4	=A2.groups(custkey.city;sum(amount))

With a dimension table where the primary key values are numberized, the creation of hash index (step 2) is unnecessary.

The foreign key numberization is, in essence, is a way to achieve address-alization on the external storage. The strategy converts foreign key values in the fact table into numbers, which is similar to the in-memory address-alization process, and the pre-calculation result can be reused. Note that the foreign key values in the fact table need a good sort-out whenever a major change happens to the dimension table, otherwise the correspondence could be messed up. But in real-life practices the re-matching is rare because a dimension table is relatively stable and most of the changes to it are appending and modification, instead of deletions. More documentation about engineering optimization in details handling can be found in RaqForum.

SQL is based on the concept of unordered sets. This means SQL-based databases cannot take advantage of the foreign key numberization technique to create a shortcut mechanism for locating records in an unordered set. Even if the foreign key is deliberately numberized, they cannot recognize the change but just go into the calculation and comparison of hash values. They can only employ the hash-based search.

But what if a dimension table is too large to be held by the memory?

In the above algorithm, accesses to the fact table are continuous but accesses to the dimension table are not. When we talked about hard disk characteristics, we mentioned that hard disks respond slowly to random accesses, so the algorithm is not suitable for handling a dimension table stored in the external storage.

If, from the very beginning, we store a dimension table that is already sorted by the primary key on the external storage, we can optimize performance according to the characteristics that the associative key in the dimension table is the primary key.

If the fact table is small enough to fit into the memory, the matching to records in a dimension table according to the foreign key will become an external (batch) search action. If an index is already created on the dimension table’s primary key, the search will become fast and performance is increased, by avoiding large dimension table traversal. The algorithm can be used to parse multiple foreign keys. SQL, however, does not distinguish the dimension table and the fact table. The optimized HASH JOIN will not perform HASH heaping buffering when a large table and a small table is being joined. The database will generally read the smaller table into the memory and traverse the larger table. The large dimension table traversal results in much poorer performance than the external storage search algorithm does.

If the fact table is also large, we can HASH heap the fact table only. As the dimension table is already ordered by the associative key (the primary key), we can conveniently divide it into segments, get scope values of each segment (the maximum and minimum values in each segment of primary key values), and split the fact table into heaps according to the scope values. Then we can join each heap with the corresponding segment of the dimension table. During the process we just divide the fact table into heaps physically and buffer them. There is no need to do the same actions on the dimension table. And by directly segmenting the fact table rather than using the HASH function, the unsuitable use of hash function and thus a second HASH heap action can be avoided, leading to manageable performance. The database’s HASH heaping algorithm, however, performs double heaping by dividing both large tables respectively into heaps physically and buffering them. This may result in a second heaping if we use an unsuitable HASH function and get much poorer and uncontrollable performance.

We can also turn to the cluster computing to handle a large dimension table.

Since the dimension table cannot fit into the memory of a single machine, we can put more machines in place to receive data in the table. Segment the dimension table by the primary key values and store the segments onto memories of multiple machines to form a cluster dimension table, on which we can apply the above algorithm catering to an in-memory dimension table to parse multiple foreign keys at a time and make parallel processing easy to perform. The foreign key numberization technique can be applied to a cluster table, too. With this algorithm, the fact table will not be transmitted, only a small amount of network transmission is generated, and no nodes are need to buffer data locally. Under the SQL system, we do not know which is the dimension table, and HASH splitting method performs Shuffle action on both tables, which produces a lot more network transmission.

As a lot of details are involved in the algorithm and due to limited space, here we just skip them. Just visit RaqForum to find more related essays if you are interested.

Ⅷ Order-based Merge Join

Now, we look at how to optimize and speed up homo-dimension table JOINs and primary-and-sub table JOINs. They share the same optimization method.

As we mentioned, HASH JOIN algorithm’s computational complexity degree (the number of comparisons between associated fields) is about SUM(nimi), which is much smaller than nm, the degree of complexity for performing a full traversal. Yet, you need to choose the right HASH function to get your luck.

If both tables are ordered by the associative fields, we can use the merge-join algorithm to handle a JOIN. The complexity degree is n+m. When both n and m are large (usually they are much larger than the value range of a HASH function), the complexity degree is far smaller than that of HASH JOIN algorithm. There are already a lot of discussions about the merge-join algorithm, so we won’t go into details.

Yet, this isn’t the right algorithm to handle foreign-key-based joins because there might be multiple foreign keys in a fact table that participate in the join process and the fact table can’t be ordered by all of them at the same time.

But it is a suitable algorithm for handling joins between homo-dimension tables and between primary and sub tables.

Besides the primary key in one table, the joining field in the other table is always the primary key for the homo-dimension table joins or a part of the primary key for primary and sub table joins. We can pre-sort the to-be-associated tables by their primary keys. Though the sorting is time -consuming, it is once and for all. With the ordered tables, we can always handle JOINs in later computations using the merge-join algorithm, which can considerably increase efficiency.

Another time an algorithm can be designed because we are able to make use of the important computing feature, that is, joining keys are primary tables, or the primary key and a part of the primary key.

The importance of order-based merge algorithm lies in the handling of large amounts of data. A pair of primary and sub tables, say, an orders table and an order detail table, are ever-increasing fact tables, which, in the course of time, often become huge and exceeds the memory capacity.

The HASH heaping method targeting at external storage data processing generates too much buffered data and has high IO load resulted from two rounds of reads and one write on the disk. There isn’t such performance issue with the order-based merge algorithm. Each of the two tables being joined needs one traversal only. Both the CPU’s computational workload and the disk IO activities will significantly decrease. The execution of order-based merge algorithm involves very small memory usage by keeping a small number of buffer records for each table. This almost won’t affect the memory demand of other concurrent tasks. The HASH heaping method requires relatively large memory for storing more retrieved data to reduce heaping activities.

The Cartesian-product-based SQL JOINs don’t define join types. Without the definition of primary-key-based joins, we can only turn to engineering optimizations but can’t devise a more efficient order-based algorithm. Some database products are designed to check if the to-be-joined tables are physically ordered by their primary keys, and use the merge-join algorithm if the result is true. The problem is unordered-set-based relational databases won’t proactively ensure that data is physically ordered; rather, many of their operations will damage the conditions for performing a merge-join algorithm. An index makes the data logically ordered, but the traversal of physically unordered data is still slow.

The condition of using order-based merge algorithm is that data tables being joined are already ordered by the primary keys. Usually, more data is consecutively appended to the ordered data tables. In principle, sorting is needed after each append. Yet the sorting of a huge data table is time -consuming. So, isn’t necessarily difficult to do the appending? In fact, combining the appended data with the existing data is also an order-based merging. Different from the regular big data sorting that needs to write data to buffer and then read it from the buffer, sorting the newly-appended data and then merging it with the ordered historical data is equivalent to writing all data again, whose complexity degree is linear. Some engineering optimization plans even make it unnecessary to write all data every time, further enhancing the maintenance efficiency. Find related documentation in RaqForum.

Another merit of the order-based merge algorithm is that it facilitates data segmentation for parallel processing.

Contemporary computers are equipped with multicore CPUs as well as SSDs that support concurrency excellently, offering solid foundation for performing multithreaded parallel processing to boost performance strongly. The conventional HASH heaping algorithm, however, is difficult to be paralleled. To perform the algorithm with parallel threads, the multiple threads will write data into a data heap at the same time, resulting in resource conflict; and the subsequent join between heaps of the two tables will use up a large memory space, affecting the number of parallel tasks.

The order-based merging will divide data into a number of segments. It’s relatively simple to partition one table. But it’s a must that data be always aligned when two tables to be associated are partitioned. Otherwise mismatch of data in the two tables will occur and the final result will be wrong. Pre-ordering data thus can ensure high-performance real-time alignment division.

To achieve the real-time alignment division between the two tables to be joined, we can first partition the primary table (or the bigger one of the two homo-dimension tables) evenly, get the primary key value in the first record of each segment to match records of the sub table (or the other homo-dimension table) using the binary search to locate the segmentation point in the second table (which is also ordered). This way the two tables will be segmented in alignment.

Since the primary key values are ordered, the key values in each segment of the primary table belong to one continuous interval, excluding records whose key values are not within the interval and ensuring the inclusion of all records whose key values are in it. Conversely, that is also the case in the sub table. Data won’t be mismatched. It is also because of the ordered key values that we can quickly locate the segmentation points in the sub table with the efficient binary search. Orderliness is thus the guarantee of proper and efficient partitioning, making it easy to perform parallel processing.

Another feature of the primary-key-based join between the primary and sub tables is that one sub table has only one primary table with which it will be joined according to the primary key (the same as the join between homo-dimension tables, but it is easy to explain the mechanism behind it using the primary and sub tables). It is impossible for a table to have multiple primary tables that don’t have any relationship between them (though the primary table may have its own primary table). In this case, we can employ the integration storage mechanism to store each record in the sub table as a field value in the corresponding record in the primary table. In this way, better performance is achieved when big data is involved as data to be stored is reduced (as the joining keys just need to be stored once) and pre-join is done without any key value matching actions.

All the join query optimization strategies mentioned previously have already been implemented in esProc SPL and found their effective applications in real-world scenarios. Now SPL is open sourced, and download and more documentation are available in Scudata, Raqsoft or RaqForum.

Conclusion

JOIN queries are the most complex database computations. In this essay, we try our best to explore and dissect them and propose our solutions but still there are aspects we haven’t cover.

More related documentation can be obtained in RaqForum.

Here is ariticle about DQL: DQL.pdf