SPL Programming Exercise - Chapter 6 Reuse
6.1 User-Defined Functions
1. Write a function for calculating the cube of integers, and calculate the cube difference between each number from 1 to 10 and its previous adjacent integer.
For example, 2, the previous adjacent number is 1, the cube difference between the two is equal to 7.
2. Write a function to convert Fahrenheit temperature to Celsius temperature, with the formula C=(F-32) * 5/9, and call the function to calculate the Celsius temperature corresponding to 73 ℉.
3. Write a function to calculate the area of a triangle using its side length.
Given three sides, determine if a triangle can be formed, and if so, calculate the area.
Tip: The formula for calculating the area of a triangle using its side length is Helen’s formula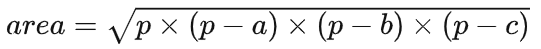
, p is half of the perimeter.
4. Use a custom function to calculate the volume of a hollow cylinder. Enter the outer radius R, inner radius r, and height h to calculate the volume.
Tip: Volume of cylinder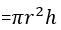
5. Customize a function to calculate BMI, input height and weight, and output BMI
6. If a number is exactly equal to the sum of all its factors, it is called a “perfect number”. For example, 6=1+2+3.
How to determine the perfect number, Euclidean discovered that as long as 2n-1 is a prime number, 2n-1(2n-1)must be a perfect number (n>=2). Write a program to find the smallest 5 perfect numbers. Require to use custom function to determine whether 2n-1 is a prime number.
7. Implement a function that can count the number of times a number appears in any integer. For example, in -21252, if 2 appears 3 times, the function should return 3.
8. Find the roots of equation ax^2 + bx + c = 0. The parameters a, b, and c are input from the main function.
6.2 Recursion
1. Write a recursive function that returns the maximum common divisor of integers x and y
2. The monkey picked a bunch of peaches and ate half of them on the first day, feeling unsatiated, the monkey ate another one; The next day, the monkey ate half of the remaining peaches and one extra; From then on, it was like this every day, by the tenth day, there was only one peach left. How many peaches were there initially?
3. A frog can jump up one or two steps at a time. How many jumping methods are there for the frog to jump up an n-level step.
4. Use recursive thinking to output a positive integer in reverse order. For example, given a positive integer n=12345, it is desired to output in reverse order of each digit, i.e. output 54321
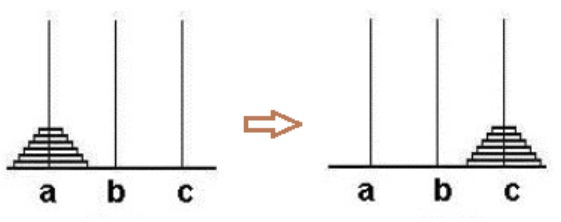
5. Hanoi Tower problem: Given three pillars, denoted as a, b, c, where there are n plates on pillar a, and the plates on top must be smaller than those below. Question: How many times does it take to move the plates on pillar a through pillar b to pillar c at least?
When moving, attention should be paid to:
① Only one plate can be moved at a time
② A large plate cannot be placed on top of a small plate
6.3 Reusable script
1. Edit the method of calculating triangle area using side length into a reusable script and call it.
2. Edit the calculation method of BMI into a reusable script and call it.
Suggested answers:
6.1 User-Defined Functions
1.
| A | B | |
|---|---|---|
| 1 | func | return A1*A1*A1 |
| 2 | =10.(func(A1,~)-func(A1,~[-1])) |
2.
| A | B | |
|---|---|---|
| 1 | func | return (A1-32)*5/9 |
| 2 | =func(A1,73) |
3.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | func | |||
| 2 | if A1 + B1 > C1 && A1 + C1 > B1 && B1 + C1 > A1 | =A1+B1+C1 | =C2/2 | |
| 3 | =sqrt(D2*(D2-A1)*(D2-B1)*(D2-C1)) | |||
| 4 | return C3 | |||
| 5 | else | return “This side length group does not form a triangle” |
4.
| A | B | C | |
|---|---|---|---|
| 1 | func | ||
| 2 | return pi()*A1*A1*C1-pi()*B1*B1*C1 |
5.
| A | B | |
|---|---|---|
| 1 | func | |
| 2 | return B1/(A1*A1) |
6.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 0 | 2 | |||
| 2 | for A1<5 | if func(A5,B1)==1 | >output(int(power(2,B1-1)*(power(2,B1)-1))) | >A1+=1 | |
| 3 | >B1+=1 | ||||
| 4 | |||||
| 5 | func | =power(2,A5)-1 | |||
| 6 | if A5==2 | return 1 | |||
| 7 | else | for 2,sqrt(B5) | if B5%C7==0 | return 0 | |
| 8 | break C7 | ||||
| 9 | return 1 |
7.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | func | 0 | ||
| 2 | if A1<0 | >A1=-A1 | ||
| 3 | if A1==0 && B1==0 | return 1 | ||
| 4 | for A1 | if A1%10==B1 | >C1+=1 | |
| 5 | >A1=10 | |||
| 6 | return C1 | |||
| 7 | =func(A1,-21252,2) |
8.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | func | |||
| 2 | if A1==0 | return -C1/B1 | ||
| 3 | else | =B1*B1-4*A1*C1 | ||
| 4 | if C3 >0 | return [(-B1+sqrt(C3))/(2*A1),(-B1-sqrt(C3))/(2*A1)] | ||
| 5 | else if C3==0 | return -B1/(2*A1) | ||
| 6 | else | return “There are no real roots” | ||
| 7 | =func(A1,3,8,5) |
6.2 Recursion
1.
| A | B | C | |
|---|---|---|---|
| 1 | func | ||
| 2 | if B1==0 | return A1 | |
| 3 | else | return func(A1,B1,A1%B1) | |
| 4 | =func(A1,54,63) |
2.
| A | B | C | |
|---|---|---|---|
| 1 | func | ||
| 2 | if A1==1 | return 1 | |
| 3 | return (func(A1,A1-1)+1)*2 | ||
| 4 | =func(A1,10) |
3.
| A | B | C | |
|---|---|---|---|
| 1 | func | ||
| 2 | if A1==1 | return 1 | |
| 3 | elseif A1==2 | return 2 | |
| 4 | else | return func(A1,A1-1)+func(A1,A1-2) | |
| 5 | =func(A1,9) |
4.
| A | B | C | |
|---|---|---|---|
| 1 | func | if A1<10 | return output(A1%10) |
| 2 | =output(A1%10) | ||
| 3 | return func(A1, A1\10),B2 | ||
| 4 | =func(A1,12345) |
Recursive thinking: First output the single digit of this number, and then output the single digit of the preceding number until there are no numbers before.
5.
| A | B | C | |
|---|---|---|---|
| 1 | func | if A1==1 | return 1 |
| 2 | return 2*func(A1,A1-1)+1 | ||
| 3 | =func(A1,10) |
SPL Official Website 👉 https://www.scudata.com
SPL Feedback and Help 👉 https://www.reddit.com/r/esProcSPL
SPL Learning Material 👉 https://c.scudata.com
SPL Source Code and Package 👉 https://github.com/SPLWare/esProc
Discord 👉 https://discord.gg/2bkGwqTj
Youtube 👉 https://www.youtube.com/@esProc_SPL



Chinese version